푸리에 급수와 푸리에 변환 완전 정복(예제pdf)

August 6, 2025

왜 푸리에 해석이 중요한가?

실제 세계에서 우리는 다양한 신호를 접하게 됩니다. 음악, 음성, 영상, 전자기파, 온도 변화 등 이 모든 것들은 시간에 따라 변하는 신호이며, 이러한 신호를 수학적으로 해석하고 처리하기 위해 푸리에 해석(Fourier Analysis) 기법이 필수적으로 사용됩니다.

푸리에 해석은 크게 두 가지로 나뉩니다.

푸리에 급수 (Fourier Series): 주기적인 신호를 해석하는 방법
푸리에 변환 (Fourier Transform): 비주기적인 신호를 해석하는 방법

1. 푸리에 급수란?

1.1 개념

어떤 함수가 일정한 주기를 갖고 반복된다면, 이 함수를 사인(sine) 과 코사인(cosine) 함수의 무한한 합으로 표현할 수 있습니다. 이것이 바로 푸리에 급수입니다.

$f(t) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos \left( \frac{2 \pi n t}{T} \right) + b_n \sin \left( \frac{2 \pi n t}{T} \right) \right)$

여기서

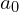$a_0$ 는 평균값(DC 성분)
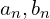$a_n, b_n$ 는 각각의 진동 성분의 크기를 나타냅니다.
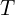$T$ 는 신호의 주기입니다.

이 계수들은 다음과 같이 계산합니다.

$a_0 = \frac{1}{T} \int_{0}^{T} f(t) , dt$

$a_n = \frac{2}{T} \int_{0}^{T} f(t) \cos\left( \frac{2 \pi n t}{T} \right) dt$

$b_n = \frac{2}{T} \int_{0}^{T} f(t) \sin\left( \frac{2 \pi n t}{T} \right) dt$

1.2 예제: 구형파(Square Wave)

아래는 주기 $2L$ 를 갖는 구형파의 예입니다.

$f(t) = \begin{cases} 1, & -L < t < 0 \ -1, & 0 < t < L \end{cases}$

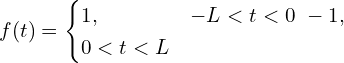
푸리에 급수 전개 결과는 다음과 같습니다:

항목	푸리에 급수	푸리에 변환
대상 신호	주기함수	비주기 함수
표현 방법	무한 사인/코사인 합	적분을 통한 주파수 표현
결과물	이산적인 주파수 성분	연속적인 주파수 성분
응용 분야	회로분석, 진동 해석	영상처리, 통신, 스펙트럼 분석

analtech

푸리에 급수와 푸리에 변환 완전 정복(예제pdf)

왜 푸리에 해석이 중요한가?

1. 푸리에 급수란?

1.1 개념

1.2 예제: 구형파(Square Wave)

2. 푸리에 변환이란?

2.1 개념

2.2 예제: 단위 임펄스 함수

3. 푸리에 급수와 변환의 차이점

4. 푸리에 해석의 활용 예시

4.1 전자회로

4.2 통신

4.3 영상 처리

5. 푸리에 급수 시각화

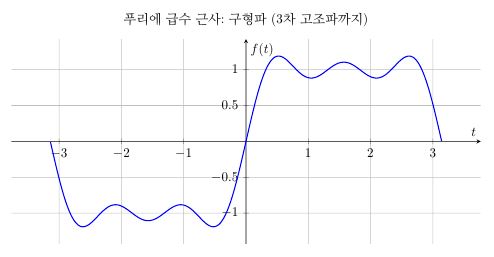
6. 마무리 요약

Leave a Reply Cancel reply