보드선도(Bode Plot)란 무엇인가?
보드선도는 제어공학이나 신호처리 분야에서 시스템의 주파수 응답 특성을 시각적으로 표현한 도구입니다. 이 선도는 로그 스케일을 사용하여 주파수에 따른 **크기(Magnitude)**와 **위상(Phase)**의 변화를 각각의 그래프로 나타냅니다.
보드선도는 두 개의 그래프로 구성됩니다:
- 크기 응답 (Magnitude Plot):
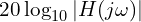
- 위상 응답 (Phase Plot):
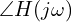 (단위는 도 또는 라디안)
(단위는 도 또는 라디안)
이 두 그래프는 복소수 전달함수 ![]() 에서
에서 ![]() 로 대입하여 얻은 주파수 응답에 따라 그려집니다.
로 대입하여 얻은 주파수 응답에 따라 그려집니다.
보드선도가 왜 중요한가?
- 시스템 안정성 평가에 매우 유용합니다.
- 시스템의 대역폭, 여유이득(Gain Margin), 여유위상(Phase Margin) 등의 특성을 직관적으로 확인할 수 있습니다.
- 필터의 설계 및 분석, 예: 로우패스, 하이패스, 밴드패스 필터 등의 성능을 분석할 때 사용됩니다.
보드선도 작성 절차
1. 전달함수 표현
먼저 시스템의 전달함수를 ![]() 또는
또는 ![]() 형태로 표현합니다. 예를 들어 다음과 같은 전달함수를 생각해 봅시다.
형태로 표현합니다. 예를 들어 다음과 같은 전달함수를 생각해 봅시다.
![]()
이를 ![]() 로 치환하면 다음과 같습니다.
로 치환하면 다음과 같습니다.
![]()
2. 크기 응답 계산
크기 응답은 다음과 같이 계산됩니다.
![]()
이를 데시벨(dB) 단위로 변환하면:
![]()
3. 위상 응답 계산
위상 응답은 다음과 같이 계산됩니다.
![]()
보드선도 해석법
보드선도에서 중요한 해석 포인트는 다음과 같습니다:
1. 코너 주파수 (Break Frequency)
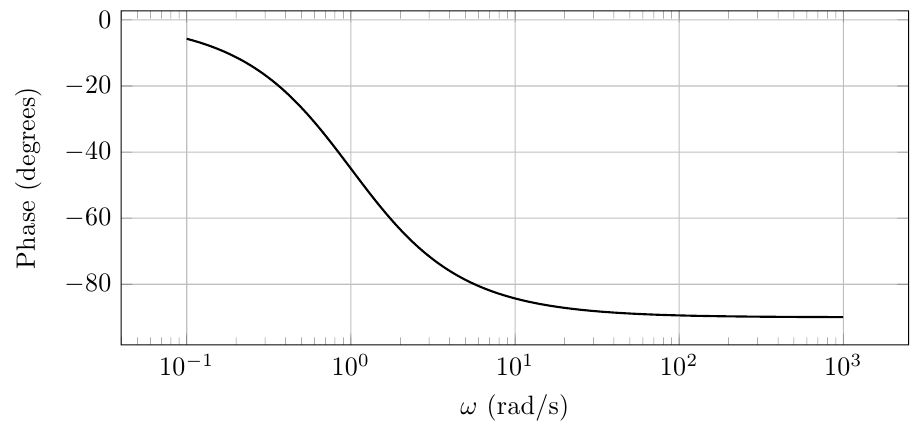
코너 주파수는 전달함수의 극점(pole)이나 영점(zero)에서 발생하는 변곡점입니다. 위 예시의 전달함수에서 코너 주파수는 ![]() 입니다. 이 주파수 이후로 기울기가 바뀝니다.
입니다. 이 주파수 이후로 기울기가 바뀝니다.
2. 기울기 분석
- 1차 극점: -20 dB/dec
- 1차 영점: +20 dB/dec
- 2차 극점: -40 dB/dec
- 2차 영점: +40 dB/dec
이 기울기 변화는 주파수 로그 축 기준으로 한 데케이드(decade; 10배 증가)마다 적용됩니다.
예제: 간단한 RC 회로
아래는 기본적인 RC 로우패스 필터 회로입니다.
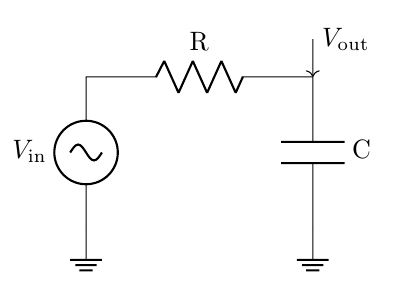
전달함수
![]()
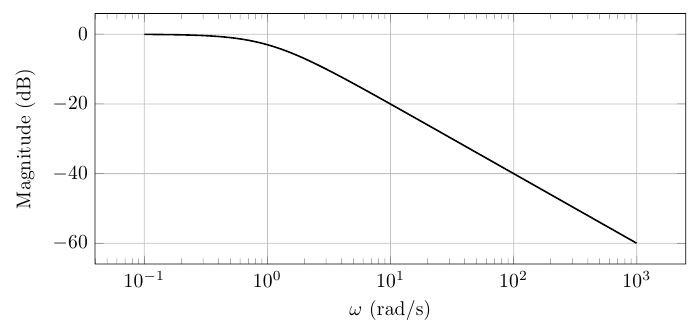
보드선도 그래프
크기 응답
위상 응답
주의사항 및 팁
- log 스케일의 축을 사용할 때,
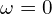 은 표현 불가능합니다. 최소
은 표현 불가능합니다. 최소 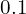 또는
또는 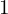 부터 시작하십시오.
부터 시작하십시오. - 복잡한 전달함수는 요소별로 나눠서 그린 후 합산하는 방식이 유리합니다. 예: 극점/영점마다 따로 그리고 겹칩니다.

Leave a Reply