라플라스 변환이란 무엇인가?
라플라스 변환(Laplace Transform)은 미분 방정식으로 표현된 시간 영역의 신호나 시스템을 복잡한 계산 없이 쉽게 분석할 수 있도록 변환하는 수학적 기법입니다. 시간 영역(Time Domain)에서 복잡하게 보이는 함수도 주파수 영역(Frequency Domain)으로 변환하면 훨씬 단순하게 해석할 수 있습니다.
전기회로, 제어공학, 신호처리 등 거의 모든 공학 분야에서 널리 사용되며, 특히 과도 응답 분석, 제어 시스템 안정성 분석, 회로 해석에 없어서는 안 될 도구입니다.
라플라스 변환의 정의
라플라스 변환의 일반적인 정의는 다음과 같습니다.
![]()
여기서,
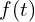 는 시간 영역의 함수
는 시간 영역의 함수 는 복소수 영역의 변수로,
는 복소수 영역의 변수로, 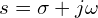 형태
형태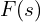 는 라플라스 변환된 함수
는 라플라스 변환된 함수
즉, 함수 ![]() 를
를 ![]() 영역으로 변환하는 것입니다.
영역으로 변환하는 것입니다.
왜 라플라스 변환이 필요한가?
예를 들어, 다음과 같은 미분 방정식이 있다고 가정해 봅시다.
![]()
이 식을 라플라스 변환하면 다음과 같이 단순한 대수 방정식으로 바뀝니다.
![]()
복잡한 미분 연산이 ![]() 를 활용한 단순한 곱셈으로 바뀌는 것을 볼 수 있습니다. 이것이 라플라스 변환의 핵심 장점입니다.
를 활용한 단순한 곱셈으로 바뀌는 것을 볼 수 있습니다. 이것이 라플라스 변환의 핵심 장점입니다.
기본 라플라스 변환 공식
대표적인 함수들의 라플라스 변환 결과는 다음과 같습니다.
| 시간 함수 | 라플라스 변환 |
|---|---|
라플라스 변환의 선형성
라플라스 변환은 선형 연산입니다. 즉,
![]()
이는 공학적 시스템의 해석에 있어 매우 유용한 특성입니다.
미분과 적분의 라플라스 변환
다음은 시간 영역에서의 미분, 적분에 대한 라플라스 변환 법칙입니다.
미분
![]()
![]()
적분
![]()
시프트 정리 (Shift Theorem)
시간 지연 혹은 지연 응답을 해석할 때 자주 사용하는 정리입니다.
시간 지연
![]()
주파수 시프트
![]()
주로 사용하는 라플라스 역변환 표
![]() 에서
에서 ![]() 로 다시 변환하는 과정이 역변환입니다. 복잡한 식일 경우 부분 분수로 분해한 후, 표를 참고하여 변환합니다.
로 다시 변환하는 과정이 역변환입니다. 복잡한 식일 경우 부분 분수로 분해한 후, 표를 참고하여 변환합니다.
라플라스 변환의 회로 해석 적용 예시
예시 회로 설명
다음은 간단한 RLC 직렬 회로의 예입니다.
- 저항:
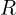
- 인덕터:
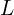
- 커패시터:
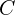
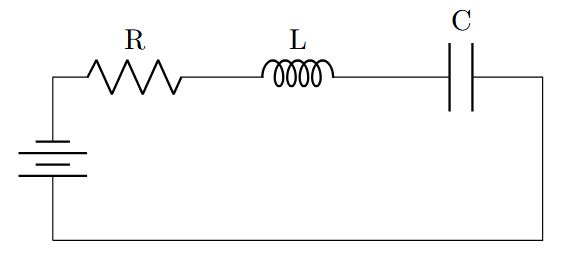
이 회로에 ![]() 를 인가하면, 다음의 미분 방정식이 성립합니다.
를 인가하면, 다음의 미분 방정식이 성립합니다.
![]()
라플라스 변환을 적용하면 다음과 같습니다.
![]()
이제 ![]() 를 쉽게 구할 수 있으며, 필요시
를 쉽게 구할 수 있으며, 필요시 ![]() 로 역변환하여 시간 영역 해석도 가능합니다.
로 역변환하여 시간 영역 해석도 가능합니다.
실제 응용 분야
- 제어 시스템 설계: 전달함수 기반 제어기 설계
- 전기 회로 해석: RLC 회로, 과도 상태 해석
- 기계 진동 분석: 감쇠 진동, 외란 응답 해석
- 신호처리: 필터 설계, 신호 응답 해석
라플라스 변환의 장단점
| 장점 | 단점 |
|---|---|
| 미분 방정식을 대수방정식으로 단순화 | 초기 조건을 반드시 명확히 알아야 함 |
| 시스템 응답을 해석하기 쉬움 | 비선형 시스템에는 적용 어려움 |
| 주파수 영역에서 시스템 특성 분석 가능 | 시불변 시스템에만 주로 사용 |
결론
라플라스 변환은 시스템 해석의 강력한 도구이며, 제어공학, 회로이론, 신호처리 등 다양한 공학 분야에 필수적으로 사용됩니다. 초보자에게는 다소 복잡해 보일 수 있지만, 위의 공식들과 성질들을 충분히 익히고 다양한 예제를 반복적으로 풀어본다면 누구나 마스터할 수 있습니다.

Leave a Reply