1. 개요
회로에서 과도응답(transient response) 은 회로에 갑자기 전압이나 전류가 인가될 때 전압·전류가 안정 상태로 수렴해 가는 과정을 말합니다. 과도응답을 이해하면 회로의 동작 특성, 안정성, 시간 지연 등을 예측할 수 있어 회로 설계에 필수적입니다.
특히 일차 회로(저항‑콘덴서 또는 저항‑인덕터)와 이차 회로(RLC 회로)의 과도응답은 전자회로 설계, 제어 시스템, 신호 처리, 전력 시스템 등 다양한 분야에서 기본이 됩니다.
2. 일차 회로의 과도응답
일차 회로는 하나의 에너지 저장 소자(C 또는 L)와 저항 R으로 이루어진 회로입니다.
2.1. RC 회로의 과도응답
RC 직렬 회로에 계단전압이 걸릴 때 커패시터 전압 vC(t)v_C(t)vC(t) 은 다음과 같습니다:
![]()
여기서 VfinalV_{\text{final}}Vfinal 은 최종 안정 전압, RCR CRC 는 시정수(time constant) τ\tauτ 입니다. 시정수가 작으면 빠르게 안정화되고, 크면 천천히 변화합니다.
또한 방전 시에는:
![]()
이렇게 지수적으로 감소합니다.
- 초보자 설명: 커패시터는 전하를 저장하고, 저항 R 은 흐름을 제한합니다. 계단 입력 후 전압 변화는 처음엔 빠르다가 시정수에 다가갈수록 느려지는 곡선 형태를 띕니다.
- 그래프 코드:
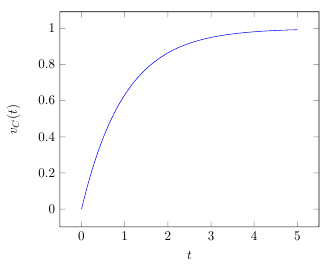
여기서는 시정수 τ=RC=1\tau = RC = 1τ=RC=1 단위로 가정하고 그렸습니다.
2.2. RL 회로의 과도응답
RL 직렬 회로에서는 인덕터 전류 iL(t)i_L(t)iL(t) 가 다음과 같습니다:
![]()
시정수는 τ=L/R\tau = L / Rτ=L/R 이고, 전류는 지수적으로 증가합니다. 전원이 제거되면:
![]()
따라서 RL 회로도 비슷한 방식으로 지수 응답을 보입니다.
3. 이차 회로의 과도응답 (RLC 회로)
이차 회로는 저항 R, 인덕터 L, 커패시터 C 로 구성되며, 과도응답의 형태는 감쇠비에 따라 크게 세 가지로 나뉩니다.
3.1. 회로 방정식
RLC 직렬 회로에서 인덕터 전류 i(t)i(t)i(t) 에 대한 미분 방정식은:
![]()
특히 계단 입력 Vin(t)=V0 u(t)V_{\text{in}}(t) = V_0\,u(t)Vin(t)=V0u(t) 에 대한 응답을 분석합니다.
3.2. 감쇠비 ζ 와 고유주파수 ω₀
정상 상태 분석을 위해 다음을 정의합니다:
![]()
이때 응답 형태는 ζ 에 따라 달라집니다.
- ζ < 1: 저감쇠 (Underdamped) → 진동 후 수렴
- ζ = 1: 임계감쇠 (Critically damped) → 빠른 수렴, 진동 없음
- ζ > 1: 과감쇠 (Overdamped) → 비진동적, 천천히 수렴
3.3. 저감쇠 경우
![]() 인 경우:
인 경우:
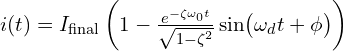
여기서 ωd=ω01−ζ2\omega_d = \omega_0 \sqrt{1-\zeta^2}ωd=ω01−ζ2, 초기 위상 ϕ\phiϕ 는 초기 조건에 따라 결정됩니다.
3.4. 임계감쇠 경우
![]() 일 때:
일 때:
![]()
가장 빠르게 진동 없이 안정 상태에 도달합니다.
3.5. 과감쇠 경우
![]() 인 경우:
인 경우:
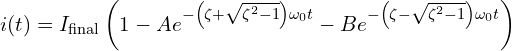
여기서 상수 A, B 는 초기 조건에 따라 결정됩니다.
3.6. 회로도 및 그래프 코드 예시
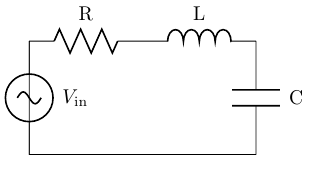
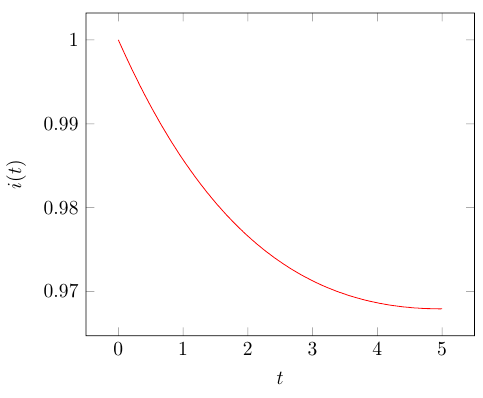
회로도에서 저항, 인덕터, 커패시터에는 문자만 사용했습니다.
4. 초보자도 이해할 수 있게 단계별 설명 요약
- 시정수와 감쇠비 개념을 이해한다.
- 저감쇠, 임계감쇠, 과감쇠 세 가지 경우를 비교한다.
- 수식 응답 형태를 보고 그래프와 연관지어 이해한다.
- 회로도를 직접 보고 흐름(전압 또는 전류)이 시간에 따라 어떻게 변하는지 상상한다.
- 실습 문제를 통해 개념을 다진다.
5. 정리
- 일차 회로(RC, RL) 는 단일 지수응답이며, 시정수 RCRCRC 또는 L/RL/RL/R 에 따라 변화 속도를 판단할 수 있습니다.
- 이차 회로(RLC) 는 감쇠비 ζ 에 따라 진동 또는 비진동 과도응답이 나타나며, ζ 에 따라 저감쇠·임계감쇠·과감쇠로 분류됩니다.
- 실제 설계에서는 목표 응답 시간, 오버슈트 허용치, 안정도 등을 염두에 두고 감쇠비와 시정수를 조절합니다.

Leave a Reply