정현파란 무엇인가?
정현파(Sinusoidal Wave)는 자연계와 공학 전반에 걸쳐 가장 기본이 되는 주기 함수 중 하나입니다. 특히 전기공학, 신호처리, 물리학 등에서 파형을 분석하고 처리하는 데 있어 중심적인 역할을 합니다.
정현파는 수학적으로 매우 간단한 형태로 표현되며, 그 단순함에도 불구하고 다양한 현상을 정확히 모델링할 수 있습니다.
정현파의 수학적 표현
정현파는 기본적으로 사인 함수나 코사인 함수로 표현됩니다. 가장 일반적인 형태는 다음과 같습니다.
![]()
또는
![]()
여기서:
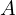 : 진폭 (Amplitude), 파형의 최대 크기
: 진폭 (Amplitude), 파형의 최대 크기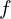 : 주파수 (Frequency), 1초당 반복 횟수
: 주파수 (Frequency), 1초당 반복 횟수 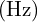
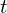 : 시간 (Time),
: 시간 (Time),  단위
단위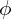 : 위상 (Phase),
: 위상 (Phase), 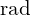 또는
또는 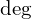
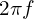 : 각속도
: 각속도  , 즉
, 즉 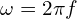
왜 정현파가 중요한가?
정현파는 다음과 같은 이유로 전기전자 분야에서 매우 중요합니다:
- 선형 시스템의 기본 해
모든 선형 시스템의 응답은 정현파 입력에 대해 예측 가능하며, 주파수 응답으로 표현할 수 있습니다. - 푸리에 해석의 기본
모든 주기적인 신호는 정현파들의 합으로 분해할 수 있으며, 이를 푸리에 급수라고 합니다. - AC 전력 시스템의 표준
교류 전력 시스템에서 사용되는 전압 및 전류는 기본적으로 정현파입니다.
시간영역과 주파수영역 표현
정현파는 시간에 따라 변화하지만, 고정된 진폭과 주파수를 갖습니다. 이를 복소수 형식으로도 표현할 수 있으며, 이 표현은 회로 해석에 매우 유용합니다.
복소수 표현:
![]()
복소수 지수 표현은 위상과 주파수를 쉽게 조작할 수 있게 해줍니다.
정현파 신호의 그래프
정현파는 아래와 같은 특징적인 그래프를 가집니다.
- 주기
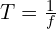
- 파형은 대칭적이며, 평균값이 0입니다.
- 한 주기 내 최대값은
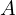 , 최소값은
, 최소값은 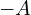 입니다.
입니다.
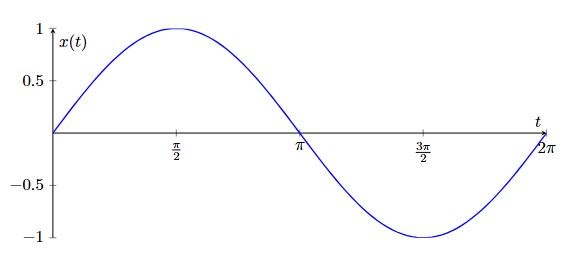
정현파의 파라미터 분석
| 항목 | 기호 | 의미 |
|---|---|---|
| 진폭 | 최대값 | |
| 주기 | 한 주기 동안의 시간 | |
| 주파수 | 1초당 반복 횟수 | |
| 각속도 | 각도 변화율 | |
| 위상 | 파형의 시작 지점 이동 |
예시: 220V 전원
일반 가정의 교류 전원은 다음과 같이 표현됩니다.
![]()
- 진폭:
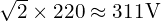
- 주파수:
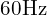
- RMS 전압:
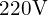
위상차와 다상 시스템
두 개 이상의 정현파가 서로 다른 위상을 가질 경우 다음과 같은 차이를 보입니다.
![]()
![]()
이것은 삼상 전원 시스템에서의 위상 차이입니다.

Leave a Reply