What Really Makes Motors Spin? A Physics Breakdown

1) Why these three ideas matter

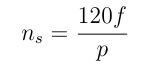
Electrical machines (motors, generators, transformers, actuators) all boil down to three physical pillars:

Rotating magnetic field (RMF) — how we create a moving magnetic pattern that pulls conductors (or rotors) around.
Flux path — how magnetic flux $\Phi$ actually travels through iron, air gaps, and windings, and how reluctance shapes it.
Electromagnetic force/torque — how current-carrying conductors in a magnetic field experience force $\mathbf{F}$ and convert electrical power to mechanical power (or the reverse).

Below, we’ll build these from first principles, give you compact but rigorous equations, and then walk through six worked problems (2 beginner, 2 intermediate, 2 advanced). Every formula and special symbol is wrapped for WP QuickLaTeX compatibility.

2) Rotating magnetic field (RMF)

In a balanced three‑phase stator, each phase current is sinusoidal, time‑shifted by $\pm 120^\circ$ , and spatially distributed by $\pm 120^\circ$ . The vector (space‑phasor) sum of these stator mmfs forms a constant‑magnitude magnetic field that rotates at synchronous speed.

The synchronous mechanical speed in rpm is

$n_s = \frac{120 f}{p}$

where

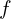$f$ = supply frequency (Hz)
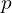$p$ = number of poles

The corresponding electrical angular speed (rad/s) is

$\omega_s = \frac{4 \pi f}{p/2} = \frac{2 \pi n_s}{60}$

In induction machines, the rotor lags the RMF, creating slip:

$s = \frac{n_s - n_r}{n_s}$

with $n_r$ the rotor mechanical speed (rpm). Slip governs rotor frequency, torque, and losses.

3) Flux path & magnetic circuits

Magnetics often parallels DC circuits:

Flux: 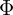$\Phi$ (Wb)
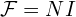MMF: $\mathcal{F} = N I$ (A‑turn)
Reluctance: 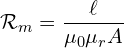$\mathcal{R}_m = \dfrac{\ell}{\mu_0 \mu_r A}$ (A‑turn/Wb)

Thus,

$\Phi = \frac{\mathcal{F}}{\mathcal{R}_m} = \frac{N I}{\mathcal{R}_m}$

Air gaps dominate reluctance because $\mu_r \approx 1$ for air, while iron has $\mu_r \gg 1$ . Consequently, tiny geometry changes in the air gap (e.g., eccentricity, saliency) strongly affect flux and torque.

For transformers (no mechanical rotation), Faraday’s law rules:

$v(t) = N \frac{d \Phi(t)}{d t}$

Sinusoidal steady‑state gives the familiar per‑turn volts:

$V_{\text{rms}} \approx 4.44 f N \Phi_{\text{max}}$

4) Electromagnetic force and torque

The Lorentz force on a conductor segment of length $\ell$ carrying current $I$ in magnetic flux density $\mathbf{B}$ :

$\mathbf{F} = I , \mathbf{\ell} \times \mathbf{B}$

In many machine models, average torque can be compactly expressed as proportional to flux and current. A classic DC torque law:

$T \approx k_t \Phi I_a$

More generally (for any electromechanical device where energy is stored magnetically), torque can be derived from co‑energy:

$T(\theta, i) = \frac{\partial W_{\text{co}}(\theta, i)}{\partial \theta}$

If inductance depends on position $\theta$ , e.g.,

$L(\theta) = L_0 + L_1 \cos(m \theta),$

then with constant current $i$ ,

$T(\theta) = \frac{1}{2} i^2 \frac{d L(\theta)}{d \theta}.$

This underpins torque production in reluctance motors, stepper motors, and synchronous machines with saliency.

For synchronous machines, the well‑known power‑angle relation (neglecting resistance) is

$P_e = \frac{3 V E}{X_s} \sin \delta, \qquad T_e = \frac{P_e}{\omega_s}$

with $V$ the stator terminal voltage magnitude, $E$ the internal emf magnitude, $X_s$ synchronous reactance, $\delta$ the torque (load) angle, and $\omega_s$ the synchronous electrical rad/s.

5) How these appear in real machines

Induction motors: RMF induces rotor currents at frequency 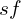$s f$ ; electromagnetic torque peaks near moderate slip; at 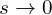$s \to 0$ (synchronous), torque → 0.
Synchronous machines: Rotor locks to the RMF ( 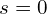$s=0$ ); torque controlled by 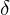$\delta$ and field excitation; stability tied to the slope of the power‑angle curve.
Reluctance & stepper motors: Torque from position‑dependent inductance; shaped salient poles create a strong $dL/d\theta$ .
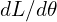Transformers: No mechanical torque, but the same flux‑linkage principles determine induced voltages, leakage reactance, and core losses.

6) Six worked problems (with full solutions)

Beginner Level (2)

B1. Synchronous speed
A three‑phase machine has $p = 4$ poles and operates from $f = 60 \text{ Hz}$ . Find the synchronous speed $n_s$ in rpm.

Solution

$n_s = \frac{120 f}{p} = \frac{120 \times 60}{4} = 1800 \text{ rpm}.$

B2. Flux in a simple core
A magnetic core (uniform cross‑section) has $N = 500$ turns, carries $I = 0.2 \text{ A}$ , mean path length $\ell = 0.3 \text{ m}$ , cross‑sectional area $A = 2.0 \times 10^{-4} \text{ m}^2$ , and relative permeability $\mu_r = 4000$ . Compute flux $\Phi$ .

Solution
Reluctance

$\mathcal{R}_m = \frac{\ell}{\mu_0 \mu_r A} = \frac{0.3}{(4\pi \times 10^{-7}) \times 4000 \times 2.0 \times 10^{-4}} \approx 0.3 \Big/ (1.005 \times 10^{-6}) \approx 2.985 \times 10^{5} , \text{A-turn/Wb}.$

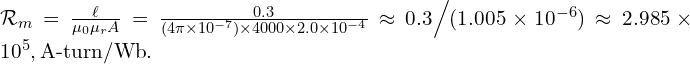
MMF

$\mathcal{F} = N I = 500 \times 0.2 = 100 \text{ A-turn}.$

Flux

$\Phi = \frac{\mathcal{F}}{\mathcal{R}_m} \approx \frac{100}{2.985 \times 10^{5}} \approx 3.35 \times 10^{-4} \text{ Wb}.$

Intermediate Level (2)

I1. Slip and rotor frequency
A 4‑pole induction motor is fed at $60 \text{ Hz}$ and runs at $n_r = 1740 \text{ rpm}$ . Find slip $s$ and rotor current frequency $f_r$ .

Solution

$n_s = \frac{120 f}{p} = \frac{120 \times 60}{4} = 1800 \text{ rpm}.$

$s = \frac{n_s - n_r}{n_s} = \frac{1800 - 1740}{1800} = \frac{60}{1800} = 0.0333 ; (3.33%).$

Rotor frequency

$f_r = s f = 0.0333 \times 60 \approx 2.0 \text{ Hz}.$

I2. Lorentz force on a bar
A straight conductor of length $\ell = 0.15 \text{ m}$ carries current $I = 25 \text{ A}$ and lies perpendicular to a uniform field $B = 0.8 \text{ T}$ . Compute the force magnitude.

Solution

$F = B I \ell = 0.8 \times 25 \times 0.15 = 3.0 \text{ N}.$

Advanced Level (2)

A1. Torque from a position‑dependent inductance
A doubly‑salient machine has
$L(\theta) = L_0 + L_1 \cos(2\theta)$
with $L_0 = 50 \text{ mH}$ , $L_1 = 10 \text{ mH}$ . It is excited by a constant current $i = 5 \text{ A}$ . Derive $T(\theta)$ and evaluate it at $\theta = 30^\circ$ .

Solution
Co‑energy for a current‑controlled device:

$W_{\text{co}}(\theta, i) = \frac{1}{2} L(\theta) i^2.$

Torque:

$T(\theta) = \frac{\partial W_{\text{co}}}{\partial \theta} = \frac{1}{2} i^2 \frac{d L(\theta)}{d \theta}.$

$\frac{d L(\theta)}{d \theta} = -2 L_1 \sin(2\theta).$

Thus,

$T(\theta) = \frac{1}{2} (5)^2 (-2 \times 10 \text{ mH}) \sin(2\theta) = -25 \times 10 \text{ mH} \sin(2\theta).$

Convert $10 \text{ mH} = 0.01 \text{ H}$ :

$T(\theta) = -25 \times 0.01 \sin(2\theta) = -0.25 \sin(2\theta) \text{ N·m (units consistent)}.$

At $\theta = 30^\circ$ , $2\theta = 60^\circ$ , $\sin 60^\circ = \frac{\sqrt{3}}{2} \approx 0.866$ :

$T(30^\circ) = -0.25 \times 0.866 \approx -0.2165 \text{ N·m}.$

The negative sign indicates the torque tends to move the rotor toward decreasing co‑energy gradient (stable alignment position).

A2. Synchronous machine power‑angle torque
A round‑rotor synchronous generator has $V = 4.16 \text{ kV (L-L, rms)}$ , $E = 3.6 \text{ kV (L-L, rms)}$ , and $X_s = 1.2 , \Omega \text{ (per phase)}$ . It operates at $\delta = 25^\circ$ , $f = 60 \text{ Hz}$ , $p = 4$ . Compute electrical air‑gap power $P_e$ and torque $T_e$ .

Solution
Use phase quantities. Convert L‑L to phase (star):

$V_{\phi} = \frac{4.16 , \text{kV}}{\sqrt{3}} \approx 2.402 \text{ kV}, \quad E_{\phi} = \frac{3.6 , \text{kV}}{\sqrt{3}} \approx 2.078 \text{ kV}.$

Electrical power (neglecting resistance):

$P_e = \frac{3 V_{\phi} E_{\phi}}{X_s} \sin \delta.$

Compute:

$\frac{3 V_{\phi} E_{\phi}}{X_s} = \frac{3 \times 2402 \times 2078}{1.2} \text{ W} \approx \frac{3 \times 4.992 \times 10^6}{1.2} \approx 12.48 \times 10^6 \text{ W}.$

Multiply by $\sin 25^\circ \approx 0.4226$ :

$P_e \approx 12.48 \times 10^6 \times 0.4226 \approx 5.28 \times 10^6 \text{ W} = 5.28 \text{ MW}.$

Synchronous electrical rad/s (mechanical speed is $n_s = 1800 \text{ rpm}$ ; electrical rad/s equals mechanical rad/s times pole pairs $p/2 = 2$ , but we can more directly compute mechanical and then divide power):

Mechanical synchronous speed

$n_s = \frac{120 f}{p} = \frac{120 \times 60}{4} = 1800 \text{ rpm}.$

Mechanical rad/s

$\omega_m = \frac{2 \pi n_s}{60} = \frac{2 \pi \times 1800}{60} = 188.5 \text{ rad/s}.$

Torque

$T_e = \frac{P_e}{\omega_m} \approx \frac{5.28 \times 10^6}{188.5} \approx 28.0 \times 10^3 \text{ N·m}.$

7) Key takeaways

Three‑phase windings naturally synthesize a rotating field; pole count and frequency set $n_s$ .
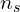Flux prefers low‑reluctance paths; the air gap dominates magnetic design.
Electromagnetic torque can be obtained from Lorentz force or co‑energy; both are consistent and invaluable, especially for salient/reluctance machines.
Practical machine equations (slip torque curves, power‑angle characteristics) are all direct consequences of these fundamentals.

25_07_28_2 Download

Electromagnetic Induction: The Basics You Must Know

What Are Electrical Machines? Full Guide for Engineers

← Prev Next →