초기조건 처리란 무엇인가?
회로 해석에서 “초기조건(initial condition)”이란, 시간 ![]() 에서 각 소자의 상태(전압 또는 전류)를 의미합니다. 특히 커패시터와 인덕터는 저장 소자(storage elements)이므로, 그 상태가 이후 회로 해석에 결정적인 영향을 미칩니다.
에서 각 소자의 상태(전압 또는 전류)를 의미합니다. 특히 커패시터와 인덕터는 저장 소자(storage elements)이므로, 그 상태가 이후 회로 해석에 결정적인 영향을 미칩니다.
초기조건을 올바르게 처리하지 않으면 과도해석(transient analysis) 결과가 왜곡되며, 실제 회로 동작과 전혀 다른 결과를 초래할 수 있습니다. 따라서 전기전자 회로 해석에서 초기조건은 기초이자 핵심 개념입니다.
왜 초기조건이 중요한가?
RLC 회로와 같은 2차 회로는 미분 방정식을 통해 해석됩니다. 이때 미분 방정식의 해는 두 부분으로 나뉩니다:
- 자연해 (Homogeneous solution): 회로에 저장된 에너지가 만들어내는 응답.
- 강제해 (Particular solution): 외부에서 주어지는 입력이 만들어내는 응답.
자연해는 초기조건에 따라 결정되므로, 초기조건은 전체 응답을 좌우합니다. 특히 ![]() -도메인에서 해석하는 라플라스 변환 방식에서는 초기조건을 변환하여 수식에 직접 반영합니다.
-도메인에서 해석하는 라플라스 변환 방식에서는 초기조건을 변환하여 수식에 직접 반영합니다.
저장 소자의 초기조건
1. 커패시터 (Capacitor)
커패시터의 전압은 불연속적으로 변화할 수 없습니다. 즉, 다음 식이 성립합니다:
![]()
커패시터의 전류-전압 관계는 다음과 같습니다:
![]()
커패시터는 전압을 기억하므로, 전압의 초기값 ![]() 은 이후 해석에 반드시 사용됩니다.
은 이후 해석에 반드시 사용됩니다.
2. 인덕터 (Inductor)
인덕터의 전류 역시 불연속적으로 변화할 수 없습니다:
![]()
인덕터의 전압-전류 관계는 다음과 같습니다:
![]()
즉, 인덕터는 전류를 기억하며, 초기 전류 ![]() 는 해석에 매우 중요합니다.
는 해석에 매우 중요합니다.
시간영역 vs. 주파수영역에서의 초기조건 처리
시간영역 처리법
미분방정식 또는 노달 해석 시, 시간에 대한 초기조건을 직접 적용합니다.
예: 커패시터가 ![]() 라면, 시간
라면, 시간 ![]() 부근에서 전류를 유도할 수 있습니다:
부근에서 전류를 유도할 수 있습니다:
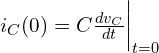
라플라스 변환을 통한 주파수영역 처리법
라플라스 변환을 사용하면 미분방정식을 대수방정식으로 변환할 수 있습니다. 이때 초기조건은 다음과 같이 포함됩니다:
- 커패시터:
![]()
- 인덕터:
![]()
이 초기조건 항들은 등가회로로도 표현 가능합니다.
초기조건을 포함한 등가회로 모델
회로 해석 시 라플라스 도메인으로 변환하여 초기조건을 회로 모델로 표현할 수 있습니다.
1. 커패시터의 초기조건 포함 모델
초기 전압 ![]() 를 포함하면, 커패시터는 다음과 같은 모델로 바뀝니다:
를 포함하면, 커패시터는 다음과 같은 모델로 바뀝니다:
- 커패시터:
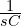 (임피던스)
(임피던스) - 초기조건 전압: 직렬 전압원
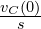
또는 병렬 전류원 모델로 변환 가능.
2. 인덕터의 초기조건 포함 모델
초기 전류 ![]() 를 포함하면, 인덕터는 다음과 같이 표현됩니다:
를 포함하면, 인덕터는 다음과 같이 표현됩니다:
- 인덕터:
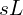 (임피던스)
(임피던스) - 초기조건: 병렬 전류원
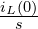 또는 직렬 전압원
또는 직렬 전압원 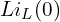
실전 예제
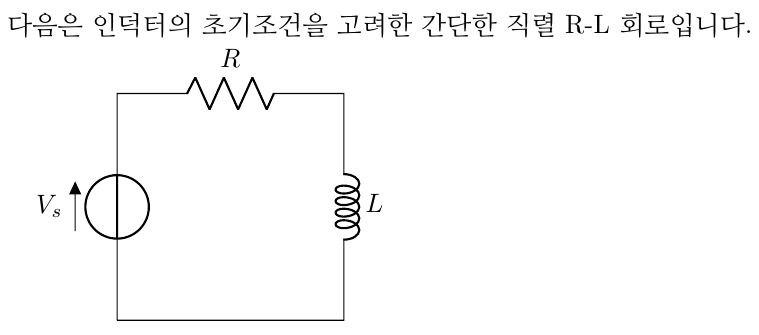
문제
아래의 회로에서 시간 ![]() 이전까지 스위치는 열려 있었고,
이전까지 스위치는 열려 있었고, ![]() 에 닫힌다. 초기조건을 포함하여
에 닫힌다. 초기조건을 포함하여 ![]() 를 구하라.
를 구하라.
- 인덕터의 초기 전류는
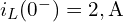
- 저항
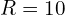 , 인덕터
, 인덕터 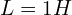
풀이
인덕터의 초기 전류 ![]() A 이므로, 스위치가 닫힌 직후
A 이므로, 스위치가 닫힌 직후 ![]() A 입니다.
A 입니다.
라플라스 변환 적용:
- 인덕터:
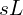 와 전압원
와 전압원 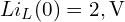
등가회로에서 전압 나눗셈으로 ![]() 를 구하고, 역변환하여
를 구하고, 역변환하여 ![]() 를 도출합니다.
를 도출합니다.
초기조건 판단 시 주의사항
- 전원 상태를 반드시 파악할 것: 스위치의 개폐 시점, 직류/교류 여부
- 소자의 특성에 따른 연속성 조건 고려: 커패시터 전압, 인덕터 전류
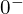 와
와 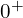 의 값은 다를 수도 있음: 외부 자극 여부 확인
의 값은 다를 수도 있음: 외부 자극 여부 확인- 회로 변경 여부 판단: 스위치 등으로 회로 구성 자체가 바뀌는 경우 해석도 달라짐
초기조건 해석의 대표적 응용 분야
- 전력전자 회로 설계
- 자동차 전장 시스템
- 임베디드 시스템의 전원 설계
- 에너지 저장 장치 분석 (배터리, 수퍼커패시터 등)
마무리 요약
- 초기조건은 커패시터 전압, 인덕터 전류와 직결
- 과도해석과 라플라스 해석에서 핵심적 역할
- 초기조건은 해석 전 반드시 계산 또는 추정 필요
- 저장 소자의 특성과 연속성 조건을 엄격히 적용

Leave a Reply