1. 서론
전기 회로에서 교류(AC) 신호를 해석할 때, 시간에 따라 변화하는 전압과 전류를 직관적으로 분석하는 것이 쉽지 않습니다. 특히 주파수가 일정한 정현파 신호에서는 페이저(Phasor)라는 복소수 표현을 사용하면 복잡한 미분 방정식 없이 회로를 간단히 해석할 수 있습니다.
이 글에서는 페이저의 정의, 수학적 배경, 그리고 실제 회로 해석에 어떻게 적용하는지를 초보자도 쉽게 이해할 수 있도록 자세히 설명합니다.
2. 페이저란 무엇인가?
페이저는 정현파 신호의 크기와 위상을 복소수로 표현한 것입니다. 예를 들어, 다음과 같은 정현파 전압이 있다고 가정합시다.
![]()
여기서 ![]() 은 최대 전압,
은 최대 전압, ![]() 는 각주파수,
는 각주파수, ![]() 는 초기 위상입니다. 이를 복소평면 상의 벡터로 표현하면,
는 초기 위상입니다. 이를 복소평면 상의 벡터로 표현하면,
![]()
여기서 ![]() 는 허수단위,
는 허수단위, ![]() 는 오일러 공식에 따라 복소수의 극형식 표현입니다. 페이저는 시간 성분(
는 오일러 공식에 따라 복소수의 극형식 표현입니다. 페이저는 시간 성분(![]() )을 제거하여 위상과 크기 정보만 남겨 회로 해석을 쉽게 합니다.
)을 제거하여 위상과 크기 정보만 남겨 회로 해석을 쉽게 합니다.
3. 페이저 표현의 수학적 배경
오일러 공식은 페이저의 기초입니다.
![]()
따라서, 원래의 시간 함수는
![]()
입니다. 이때 ![]() 가 바로 페이저입니다.
가 바로 페이저입니다.
4. 페이저 해석의 장점
- 미분·적분 계산의 단순화: 미분은
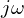 곱셈, 적분은
곱셈, 적분은 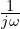 곱셈으로 변환됩니다.
곱셈으로 변환됩니다. - 복잡한 회로에서의 직관성 제공: 크기와 위상을 하나의 복소수로 처리하여 계산량 감소
- 선형 회로 해석에 최적화: 선형소자(R, L, C)에 대해 임피던스 개념 도입 가능
5. 주요 페이저 공식과 임피던스
5.1 저항기 (R)
![]()
5.2 인덕터 (L)
![]()
5.3 커패시터 (C)
![]()
6. 페이저 해석 단계
- 시간 영역의 신호를 페이저로 변환
![]()
회로 소자들을 임피던스로 변환
저항, 인덕터, 커패시터를 임피던스 형태로 표현.
복소수 회로 해석
오옴의 법칙과 키르히호프 법칙을 복소수 형태로 적용.
해석 결과를 시간 영역으로 변환
복소수 결과에서 실수부만 취해 원래의 시간 신호로 복원.
7. 페이저 해석 예제
예제 1: 단순 R-L 직렬 회로의 전류 구하기
![]()
- 각주파수:
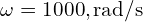
- 임피던스:
![]()
페이저 전압:
![]()
전류 페이저:
![]()
시간 영역 전류:
![]()
8. 결론
페이저 해석은 교류 회로 해석에서 필수적인 도구입니다. 이를 통해 복잡한 시간 의존 미분 방정식을 단순한 대수 계산으로 바꿀 수 있으며, 전기회로의 동작을 명확히 이해하고 설계하는 데 필수적인 기법입니다.
이 글에서는 페이저의 정의, 수학적 배경, 회로 적용 예제까지 자세히 다루었으니, 반복 학습을 통해 숙달하시길 바랍니다.

Leave a Reply