Y-Δ 변환 완전 정복: 회로 해석 초보자도 쉽게 이해하는 방법
전자회로에서 복잡한 저항망을 단순화하는 방법 중 가장 중요한 도구 중 하나가 Y-Δ 변환입니다. 특히 삼상 전원이나 브리지 회로, 복잡한 저항 네트워크에서 회로 해석을 용이하게 해주기 때문에 전기전자 공학에서는 반드시 이해해야 하는 핵심 개념입니다. 이번 글에서는 초보자도 쉽게 이해할 수 있도록 Y-Δ 변환의 원리부터 공식, 실제 회로 적용법, 그리고 다양한 예제까지 자세히 설명하겠습니다.
1. Y-Δ 변환이란 무엇인가?
Y-Δ 변환은 세 개의 저항으로 이루어진 삼각형(Δ, 델타) 회로를 별 모양(Y, 와이) 회로로, 혹은 그 반대로 변환하는 방법입니다.
이를 통해 복잡한 회로의 해석을 단순화할 수 있습니다.
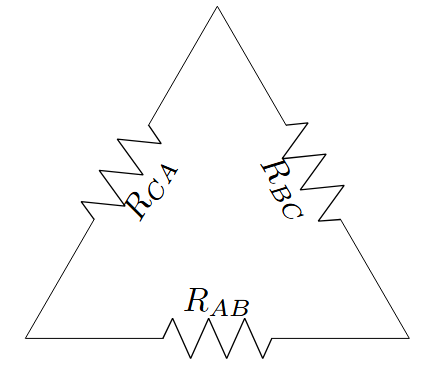
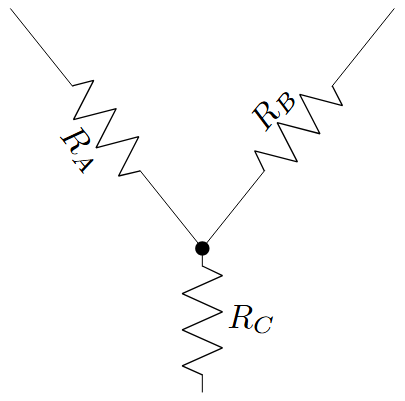
- Δ(델타) 회로: 삼각형 형태로 연결된 3개의 저항
- Y(와이) 회로: 중심점에서 3개의 저항이 방사형으로 연결된 형태
Y와 Δ 회로는 서로 등가회로가 가능하며, 변환 공식만 알면 한쪽을 다른 쪽으로 자유롭게 바꿀 수 있습니다.
2. Y-Δ 변환의 필요성
Y-Δ 변환이 필요한 이유는 주로 회로 단순화와 분석 편의성 때문입니다.
- 전류와 전압 계산이 용이
Δ 회로를 Y 회로로 변환하면 직렬·병렬로 쉽게 결합하여 총 저항을 계산할 수 있습니다. - 삼상 회로 분석
삼상 전원에서 선간 저항을 Y-Δ로 변환하면 라인 전류 계산이 간단해집니다. - 브리지 회로 해석
브리지 회로에서 Δ를 Y로 바꾸면 루프 전류를 구하기 쉬워집니다.
즉, 복잡한 연결 구조를 단순화함으로써 옴의 법칙과 키르히호프 법칙을 효율적으로 적용할 수 있습니다.
3. Y-Δ 변환 공식
3.1 Δ → Y 변환
Δ 회로의 저항 
를 Y 회로의 
로 변환할 때 공식은 다음과 같습니다.
Δ에서 Y로 변환할 때 각 Y 저항은 Δ의 인접 두 저항의 곱을 Δ 전체 합으로 나눈 값입니다.
3.2 Y → Δ 변환
반대로 Y 회로의 저항 를 Δ 회로의 로 변환할 때 공식은 다음과 같습니다.
조금 더 일반적인 형태는:
Y → Δ 변환에서는 Δ의 각 저항이 Y 저항의 전체 합 곱셈에서 특정 Y 저항으로 나누어진 값이 됩니다.
4. Y-Δ 변환 과정 예제
예제 1: Δ → Y 변환
Δ 회로의 저항이 다음과 같다고 가정합니다.
Y 회로의 저항을 구하면:
이처럼 간단한 공식 적용으로 Δ 회로를 Y 회로로 변환할 수 있습니다.
예제 2: Y → Δ 변환
Y 회로의 저항이 다음과 같다고 가정합니다.
Δ 회로의 저항은:
결과가 Δ → Y 변환 예제와 일치하여 등가 회로임을 확인할 수 있습니다.
5. 회로 해석에서 Y-Δ 변환 적용 방법
5.1 단계별 전략
- 복잡한 삼각 연결 식별
회로에서 삼각형 형태로 연결된 저항을 먼저 찾아냅니다. - 변환 유형 결정
Δ → Y로 변환할지 Y → Δ로 변환할지 결정합니다.- 병렬·직렬 합산이 쉬운 쪽으로 변환
- 공식 적용
위에서 설명한 공식으로 변환 - 회로 단순화 후 해석
변환 후 병렬/직렬 계산, 키르히호프 법칙 적용
5.2 실제 회로 예시
6. Y-Δ 변환 팁과 주의사항
- 공식 적용 시 단위 확인
저항 단위를 통일하고, 오차를 최소화합니다. - Δ → Y 변환 후 병렬/직렬 확인
변환 후 실제 회로에서 직렬·병렬 연결 여부를 반드시 체크합니다. - 삼상 회로에서는 라인과 상 전류 구분
삼상 Y-Δ 변환 시 라인 전류, 상 전류, 전압 관계를 정확히 이해해야 합니다.
Leave a Reply