Understanding AC Power: Real, Reactive, Apparent Power, and Power Factor

When you first start working with AC circuits, one of the concepts that often trips people up is power. In DC circuits, it’s pretty simple: voltage times current. But in AC, it’s not that straightforward—because the voltage and current may not always be in sync.

This is where real power, reactive power, apparent power, and power factor come in. Let’s break these down in a practical, easy-to-understand way and go through examples at the end to really lock it in.

1. What Is Real (Active) Power?

Real power, also called active power or true power, is the actual power consumed by the load to do useful work—like turning a motor or lighting a bulb.

It’s measured in watts (W).

Real power is calculated by:

  P = VI cos(θ)

Where:

2. What Is Reactive Power?

Reactive power doesn’t do any useful work—it’s the energy that flows back and forth between the source and the reactive components (inductors or capacitors).

It’s measured in volt-amperes reactive (VAR).

The formula is:

  Q = VI sin(θ)

Reactive power exists only in AC systems, not in DC, because inductance and capacitance are only reactive under changing current.

3. What Is Apparent Power?

Apparent power is the total power flowing in the circuit—whether it’s being used or not.

It’s the vector sum of real and reactive power and is measured in volt-amperes (VA).

Formula:

  S = VI
or

  S = √(P² + Q²)

It tells you the total demand your equipment places on the power system.

4. What Is Power Factor?

Power factor (PF) is the ratio of real power to apparent power. It tells you how efficiently power is being used.

  PF = P / S = cos(θ)

A power factor of 1 (or 100%) means all the power is being used effectively.
A power factor of 0.7, for example, means only 70% is doing real work, and the rest is just circulating back and forth.

Power factor is especially important in industrial setups where poor power factor can lead to penalties or inefficient operation.

5. Power Triangle

You can represent all these relationships graphically using a power triangle:

      |
      |\
    Q | \
      |  \ S
      |   \
      |    \
      -------  
        P

Where:

Beginner Example

Q1. An AC circuit has 120 V RMS voltage and draws 10 A current with a power factor of 1. What is the real, reactive, and apparent power?

Solution:

Given:

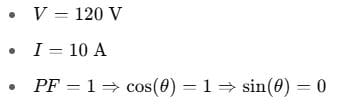
P = VI cos(θ) = 120 × 10 × 1 = 1200 W

Q = VI sin(θ) = 120 × 10 × 0 = 0 VAR

S = VI = 120 × 10 = 1200 VA

So:

• Real Power = 1200 W
• Reactive Power = 0 VAR
• Apparent Power = 1200 VA

Intermediate Example

Q2. An AC device draws 15 A current at 230 V RMS with a power factor of 0.8 lagging. Find the real power, reactive power, and apparent power.

Solution:

Given:

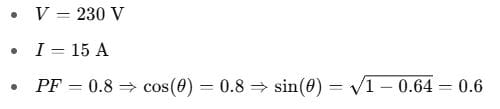
P = VI cos(θ) = 230 × 15 × 0.8 = 2760 W

Q = VI sin(θ) = 230 × 15 × 0.6 = 2070 VAR

S = VI = 230 × 15 = 3450 VA

So:

• Real Power = 2760 W
• Reactive Power = 2070 VAR
• Apparent Power = 3450 VA

Advanced Example

Q3. An industrial load has a real power of 30 kW and a reactive power of 40 kVAR. Calculate the apparent power and the power factor. Also find the phase angle θ.

Solution:

Given:

S = √(P² + Q²) = √(30² + 40²) = √(900 + 1600) = √2500 = 50 kVA

PF = P / S = 30 / 50 = 0.6

θ = cos⁻¹(0.6) ≈ 53.13°

So:

• Apparent Power = 50 kVA
• Power Factor = 0.6 lagging
• Phase angle = 53.13°

Final Thoughts

In AC systems, just looking at the voltage and current doesn’t give you the full picture. Understanding real, reactive, and apparent power, along with power factor, gives you the tools to assess how efficiently power is being used.

Industries care a lot about power factor because it affects billing, equipment sizing, and system stability. The goal is to bring the power factor as close to 1 as possible, often by using capacitor banks to cancel out inductive loads.

If you’re working with motors, transformers, or large-scale AC systems, keep this triangle in mind—it’ll serve you well.

Understanding Sinusoids and Phasor Analysis Made Simple

A Practical Guide to Impedance and Admittance Basics