Introduction

When you power up a circuit with resistors (R), inductors (L), and capacitors (C), things don’t just jump to steady-state instantly. Instead, they go through a transient response. This is especially interesting — and important — in second-order circuits, where the interaction of L and C creates oscillations, damping, or sometimes even both.

Let’s take a deep dive into how second-order RLC circuits behave during transient states, how we mathematically describe that behavior, and how you can analyze these circuits with confidence.

1. What is a Second-Order RLC Circuit?

A second-order circuit includes:

• One resistor (R)
• One inductor (L)
• One capacitor (C)

These components can be arranged in series or parallel, and both arrangements exhibit second-order differential equation behavior.

Let’s consider a series RLC circuit for simplicity, powered by a DC voltage source.

2. Deriving the Characteristic Equation

Applying Kirchhoff’s Voltage Law (KVL):

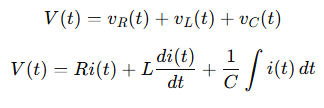
Differentiate both sides to eliminate the integral:

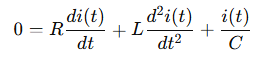
Now rearrange:

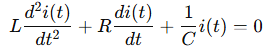
Divide everything by L:

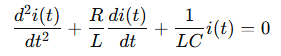
3. General Form of the Characteristic Equation

This is a second-order homogeneous differential equation:

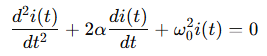
Where:

Three Cases Depending on Damping:

4. Step-by-Step Examples

Let’s practice with three example problems from beginner to advanced level.

🟢 Beginner Example: Natural Response of a Series RLC Circuit

Problem:
A series RLC circuit has R = 2Ω, L = 1H, and C = 0.25F. Find the form of the current response i(t) assuming zero input (natural response only).

Solution:

🟡 Intermediate Example: Step Response with Initial Conditions

Problem:

Solution:

The step response of an RLC circuit follows a similar form:

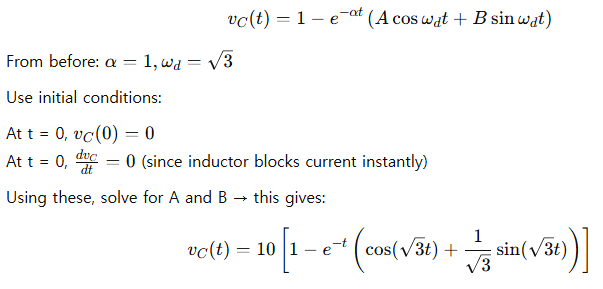
This is an oscillatory approach to 10V — classic underdamped behavior.

🔴 Advanced Example: Overdamped Case and Peak Time

Problem:

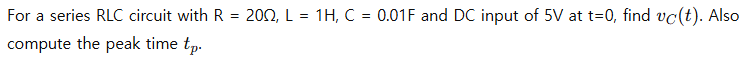
Solution:

Compute parameters:

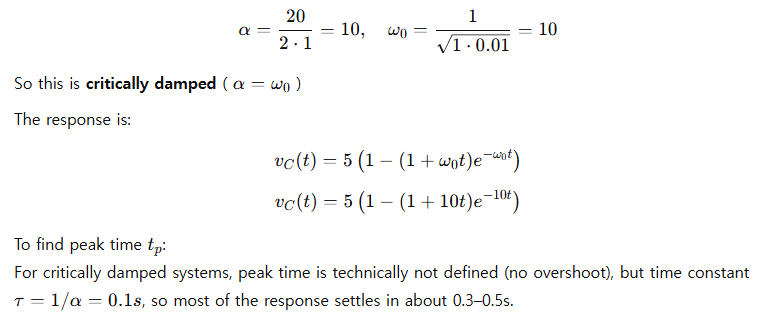
5. Practical Insights and Application

Why do we care about this?

• Circuit stability: Under- or overdamping affects stability.
• Signal response: Audio, filters, and communication circuits rely heavily on this.
• Control Systems: Similar math applies to mechanical and thermal systems.

Whenever you power up an amplifier, switch on a relay, or pulse a circuit — you’re seeing transient response in action.

6. Summary

To recap:

• Second-order circuits follow a differential equation involving R, L, and C.
• The transient response depends on damping (α) and natural frequency (ω0​).
• You can analyze the system as overdamped, critically damped, or underdamped.
• Examples show how these theoretical ideas play out in real scenarios.

Once you grasp this, analyzing real-world circuits becomes much easier — and much more interesting.

RC and RL Circuit Transients Made Simple for Beginners