Ohm’s Law: Advanced-Level Perspective
Ohm’s Law is often introduced as a basic linear relationship, but in advanced electrical engineering and applied physics, it evolves into a critical principle that underpins field theory, materials science, circuit modeling, and signal integrity analysis.
Below is an in-depth analysis for experienced engineers, researchers, or graduate-level students.
1. Generalized Form: Beyond Lumped Elements
In its elementary form, Ohm’s Law defines the ratio between voltage (V), current (I), and resistance (R):
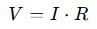
However, in the context of distributed systems or conductive media, it is expressed in its differential form using current density (𝐽) and electric field (𝐸):
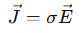

This is the foundation of Maxwell’s equations in conductive media, allowing Ohm’s Law to be applied at microscopic scales or in continuous media such as semiconductor substrates or electrolytes.
2. Frequency Domain Implications (Impedance Model)
At high frequencies, resistance alone cannot model conductor behavior. Instead, the impedance (Z) must be used, which incorporates resistance (R), inductive reactance (jωL), and capacitive reactance (1/jωC):
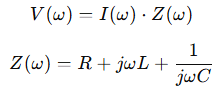
This generalized form of Ohm’s Law is crucial in AC analysis, RF circuit design, and signal integrity modeling, especially in PCB traces, cables, and transmission lines.
3. Material-Level Behavior: Nonlinearity and Temperature Effects
Real conductive materials do not always maintain a linear V−I relationship, especially under high electric fields, elevated temperatures, or in semiconductor junctions.
Temperature variation affects resistivity ρ as:

For conductors like copper or aluminum, α\alphaα is positive, meaning resistance increases with temperature — a critical factor in power electronics, motor winding design, and thermal reliability modeling.
4. Non-Ohmic Devices: Modeling and Interpretation
Ohm’s Law applies only to Ohmic materials, which exhibit linear V−I characteristics. However, most active devices — such as diodes, MOSFETs, and thyristors — are nonlinear.
For example, a diode’s current depends exponentially on the applied voltage:
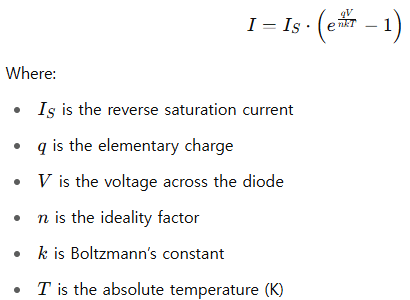
Thus, for these components, Ohm’s Law is not directly applicable — instead, characteristic equations or SPICE models are used for simulation and design.
5. Transmission Lines and Skin Effect
In high-speed digital systems, resistance is frequency-dependent due to the skin effect, which causes current to flow near the surface of the conductor at high frequencies. This results in an effective resistance R(f) that increases with frequency:
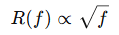
This modifies the classic Ohm’s Law because AC resistance is no longer constant — essential in the design of coaxial cables, high-speed buses, and differential pairs in PCBs.
6. Electrostatic and Quantum Considerations
In nanoelectronics or quantum transport, Ohm’s Law gives way to quantum analogs such as Landauer’s formula, which relates conductance to transmission probability in mesoscopic systems:

These models are used in quantum point contacts, graphene channels, and molecular electronics, where classical resistance loses meaning.
7. Application in Field Simulation Tools
Advanced circuit and system simulations (e.g., ANSYS, COMSOL, Keysight ADS) implement Ohm’s Law as part of finite element models or network parameter extraction. These tools calculate voltage and current distributions using:
- Material conductivity tensors
- Boundary conditions
- Coupled field equations (electromagnetic + thermal)
Engineers use Ohm’s Law in these environments to estimate voltage drops, losses, and EMI/EMC impact, often beyond what analytical solutions can deliver.
Summary
At the advanced level, Ohm’s Law is far more than V=IR. It’s a foundational concept extended into:
- Vector field relationships in continuous media
- Complex impedance in frequency-dependent systems
- Nonlinear modeling of active devices
- Quantum and nanoscale transport phenomena
Mastering its advanced forms allows engineers and physicists to design and analyze modern systems with accuracy and depth — from power grids to nanodevices.

Leave a Reply