Mastering Circuit Analysis with Laplace Transforms Step by Step

If you’ve ever found solving differential equations in circuits messy or slow, you’re not alone. The Laplace Transform is one of the most powerful tools electrical engineers use to simplify complex time-domain circuit problems into algebraic ones in the frequency (s-domain). In this post, we’ll break down what Laplace transforms are, how they’re used in circuit analysis, and work through three detailed examples — beginner, intermediate, and advanced.

Why Use Laplace Transforms in Circuit Analysis?

When you analyze circuits with capacitors and inductors, you’re often forced to deal with derivatives and integrals due to their time-domain behavior. For instance:

• An inductor’s voltage is proportional to the time derivative of current.
• A capacitor’s current is proportional to the time derivative of voltage.

This naturally leads to differential equations. But solving differential equations every time isn’t always efficient. That’s where Laplace transforms shine. They turn those calculus-heavy equations into straightforward algebra.

The Basics: Laplace Transform in a Nutshell

Laplace-Domain Equivalent of Circuit Elements

To apply Laplace transforms in circuits, you need to convert time-domain elements to their s-domain equivalents.

Step-by-Step Circuit Analysis Using Laplace

Here’s a general approach:

1. Transform the circuit into the s-domain.
2. Apply Kirchhoff’s laws (KVL or KCL) in the s-domain.
3. Solve the algebraic equations for voltages or currents.
4. Take the inverse Laplace transform to get the time-domain solution.

Example 1: Beginner Level

First-Order RC Charging Circuit

Problem:
Find the voltage across a 1 µF capacitor in a series RC circuit with R = 1 kΩ and a step input voltage

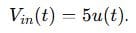
Step 1: Transform to s-Domain

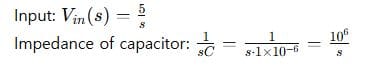
Step 2: Total Impedance

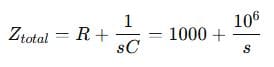
Step 3: Voltage Divider

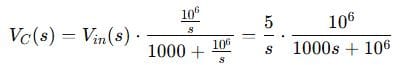
Step 4: Simplify

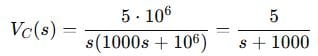
Step 5: Inverse Laplace

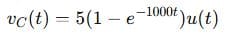
Example 2: Intermediate Level

RL Circuit with Initial Current

Problem:

Step 1: Transform

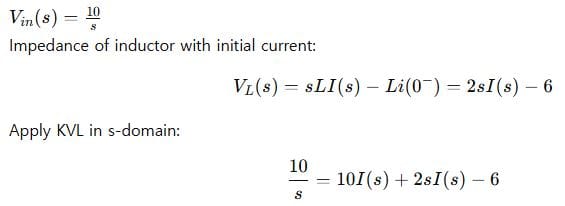
Step 2: Solve for I(s)

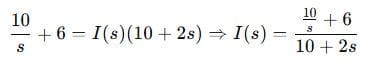
Step 3: Simplify

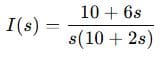
Step 4: Partial Fractions & Inverse

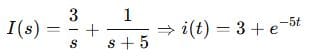
Example 3: Advanced Level

Second-Order RLC Series Circuit

Problem:
Given: R = 4 Ω, L = 1 H, C = 0.25 F

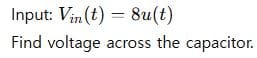
Step 1: s-Domain Transformation

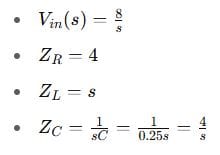
Step 2: Total Impedance

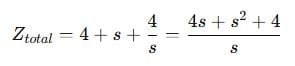
Step 3: Voltage Divider

Capacitor voltage in s-domain:

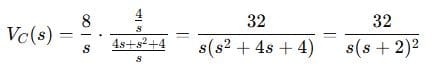
Step 4: Inverse Laplace

Use partial fractions:

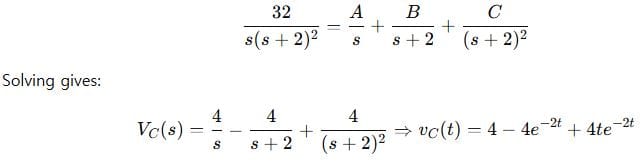
Final Thoughts

Laplace transforms are essential for engineers working with transient and frequency-domain analysis. They not only simplify the math but also provide insights into system behavior like poles, zeros, damping, and stability. As you’ve seen through these examples, whether it’s a basic RC circuit or a more complex RLC network, Laplace transforms can handle it all with elegance.

How to Calculate Power in a 3-Phase Electrical System