Mastering AC Circuits Using Complex Impedance

When dealing with AC circuits, things can get a bit tricky. Voltages and currents are no longer constant — they change over time, usually as sinusoidal waveforms. This is where complex impedance comes in as a powerful tool to simplify analysis. Instead of struggling with time-domain differential equations, we can use phasor and impedance techniques to treat AC circuits like DC ones. In this post, we’ll break down the concept of complex impedance, how it helps in AC analysis, and walk through three example problems ranging from beginner to advanced.

What is Complex Impedance?

Impedance is the AC counterpart of resistance. While resistance deals only with the real part (opposition to current), impedance handles both magnitude and phase — crucial when voltage and current are not in phase.

In phasor (frequency-domain) analysis:

Here,

This way, any RLC component in an AC circuit can be represented as a complex number.

Why Use Complex Impedance?

By converting all elements into their impedance equivalents, we can apply Ohm’s law and Kirchhoff’s rules directly — just like in DC analysis:

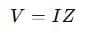
No need for time-domain integrals or derivatives. That’s a huge win.

Example 1: Beginner Level

Problem:
A resistor R=10 Ω and a capacitor C=100 μF are connected in series to a 60 Hz AC source. What is the total impedance?

Solution:

Step 1: Calculate angular frequency:

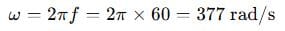
Step 2: Compute each impedance:

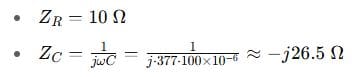
Step 3: Add impedances:

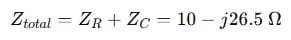
Step 4: Find magnitude and phase:

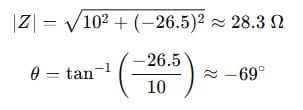
Answer:

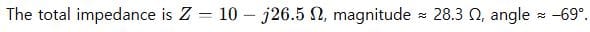
Example 2: Intermediate Level

Problem:

Solution:

Step 1: Calculate angular frequency:

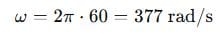
Step 2: Impedances:

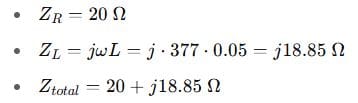
Step 3: Calculate current using Ohm’s law:

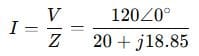
Step 4: Compute magnitude and phase:

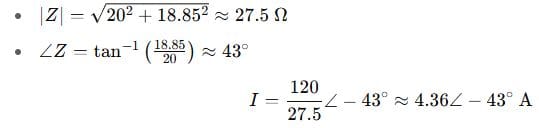
Answer:

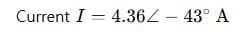
Example 3: Advanced Level

Problem:
A parallel RLC circuit is connected across a 100 V, 50 Hz source. The components are:

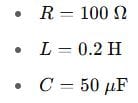
Find the total current drawn by the circuit and the overall power factor.

Solution:

Step 1: Angular frequency:

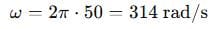
Step 2: Impedances:

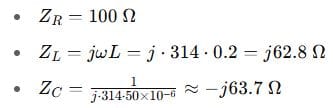
Step 3: Admittances (since parallel):

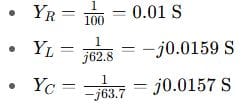
Total admittance:

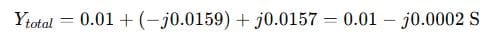
Step 4: Total impedance:

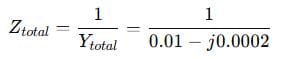
Use complex conjugate:

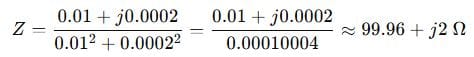
Step 5: Current:

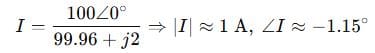
Answer:

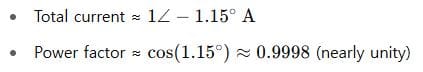
Key Takeaways

Final Thoughts

Once you get comfortable with using impedance and phasors, AC circuit analysis becomes surprisingly similar to DC circuits — just with a complex twist. Whether you’re designing filters, analyzing power factor, or calculating current in a home appliance, this method is both practical and powerful.

Let me know if you’d like to dive deeper into resonance, power factor correction, or three-phase systems using impedance next!

How to Understand Power Balance in Electrical Systems