Understanding Power Balance Conditions in Electrical Systems

If you’ve ever dived into AC circuits, you’ve probably encountered terms like real power, reactive power, and apparent power. But what about power balance? What does it mean when we say a system is “power balanced”?

In this post, we’re going to talk about what power balance means, why it matters, how it’s defined mathematically, and then walk through three example problems—ranging from basic to advanced—to make sure you’ve got it.

⚡ What is Power Balance?

In electrical systems, especially in AC circuits, the idea of power balance refers to the principle that:

The total power supplied by sources must equal the total power consumed by the loads, plus any losses (usually in the form of heat).

Mathematically, in an ideal system with no losses, we can say:

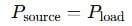
But in real-world systems, you often include line losses:

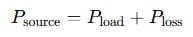
In AC systems, it’s a bit more complex because we deal with complex power:

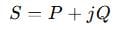
Where:

The power balance condition applies to each of these types of power, especially in power flow analysis or three-phase systems.

💡 The Role of Power Factor

Power factor (PF) is the ratio of real power to apparent power:

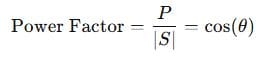
Where θ is the phase angle between voltage and current.

A system in power balance still needs a good power factor to avoid excessive current draw and system inefficiencies.

🔌 Power Balance in a Network

Let’s consider a generator supplying power to a network of resistive and reactive loads.

Let’s say:

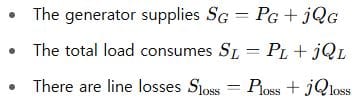
Then the power balance equation becomes:

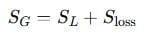
Or in components:

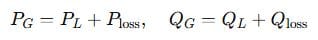
This is the formal condition for power balance.

🧪 Example 1: Beginner Level

Problem:
A simple AC circuit consumes 100 W of real power and 75 VAR of reactive power. What is the apparent power? What’s the power factor?

Solution:

We’re given:

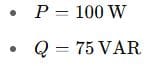
First, calculate apparent power:

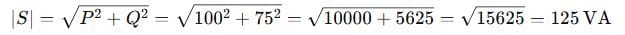
Power factor:

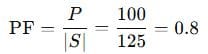
Answer:
Apparent power = 125 VA, Power factor = 0.8

🧪 Example 2: Intermediate Level

Problem:
A generator supplies 10 kW real power and 5 kVAR reactive power. The transmission line has a loss of 1 kW and 0.5 kVAR. How much real and reactive power is consumed by the load?

Solution:

We apply the power balance equation:

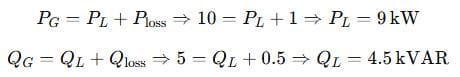
Answer:
Load consumes 9 kW and 4.5 kVAR.

🧪 Example 3: Advanced Level

Problem:
A three-phase system supplies a total of 30 kW at 0.9 lagging power factor. The total line loss is 3 kW and 2 kVAR. Calculate the total power supplied by the generator (real, reactive, and apparent), and the load power.

Solution:

Step 1: Load power

Step 2: Add line losses

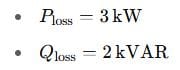
Total power supplied:

Apparent power:

Answer:
Generator supplies:

Real Power = 33 kW
Reactive Power = 16.625 kVAR
Apparent Power ≈ 36.96 kVA

🔍 Why Power Balance Matters

System Stability
If power balance isn’t maintained, voltages and currents can become unstable, risking system collapse.
Efficiency
Balanced power ensures minimal losses and optimal use of generation capacity.
Cost
Extra reactive power = more current = more loss = more money wasted on transmission and generation.

📌 Summary

Power balance means supplied power equals consumed power plus losses.
In AC systems, it’s not just real power but also reactive and apparent power that must be accounted for.
Proper balance is critical for system stability, efficiency, and safety.

Understanding Sinusoids and Phasor Analysis Made Simple

A Practical Guide to Impedance and Admittance Basics

The Truth About Reactive Power in AC Systems Explained

← Prev Next →