Introduction
Every time you flip a switch or apply power to a circuit, it doesn’t instantly reach steady state. Instead, it starts from a set of initial conditions — like the voltage across a capacitor or the current through an inductor — and then evolves over time. If you’re working with RLC circuits, differential equations, or transient analysis, initial conditions are the starting point of everything.
So today, we’ll break down:
- What initial conditions mean in circuits,
- Why they matter so much,
- How to apply them correctly,
- And we’ll solve three example problems — from easy to hard — step-by-step.
Let’s get into it.
1. What Are Initial Conditions?
In circuit analysis, initial conditions refer to the state of energy storage elements (capacitors and inductors) at the moment right before or after a switch or input changes — usually at time t=0
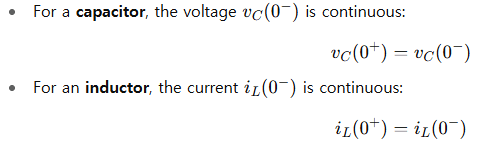
These continuity rules come from the fundamental properties:
- A capacitor cannot change voltage instantly.
- An inductor cannot change current instantly.
2. Why Are Initial Conditions Important?
Initial conditions let you solve differential equations that describe circuits. They serve as boundary values. Without them, you can’t find specific solutions — only general ones.
In practice:
- They determine transient behavior.
- They help simulate real-world startup responses.
- They affect timing in digital systems and filters.
3. Types of Initial Conditions
You usually calculate:

Other values (like derivatives) may also be needed, especially for second-order systems.
4. Step-by-Step Examples
Let’s dive into some hands-on examples.
🟢 Beginner Example: Capacitor in a DC Circuit
Problem:
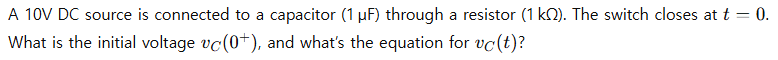
Solution:
Since the capacitor was uncharged:
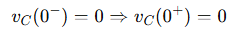
Use the classic charging equation:
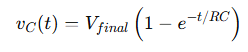
Where:
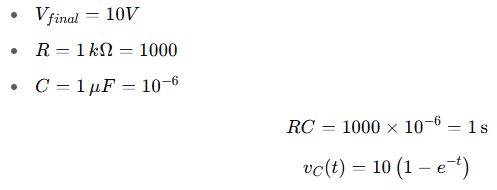
So initially:
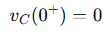
And the voltage rises to 10V over time.
🟡 Intermediate Example: Inductor Discharge
Problem:

Solution:
The key is:
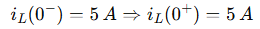
The discharge of current in an RL circuit is:
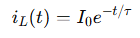
Where:
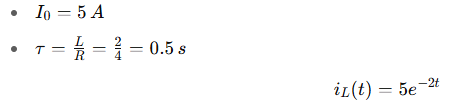
So initially, the current stays at 5A and then exponentially decays.
🔴 Advanced Example: RLC Circuit with Initial Conditions
Problem:
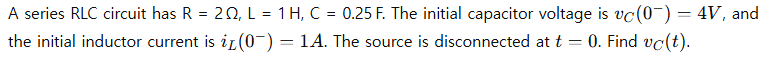
Solution:
Step 1: Use continuity:
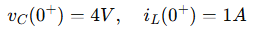
Step 2: The second-order equation:
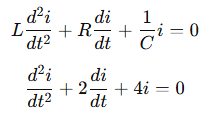
Step 3: Characteristic equation:
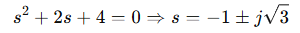
So it’s underdamped. General solution for current:
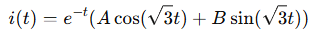
We now use initial conditions:
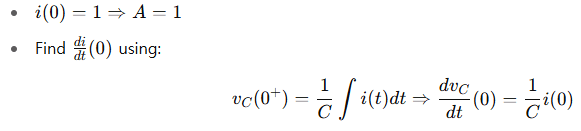
- Then, we plug into derivative and solve for B.
(Step-by-step solution would be long — the important takeaway is how we use both voltage and current initial values to fully solve the time-domain response.)
5. Tips for Solving Initial Condition Problems

6. Final Thoughts
Initial conditions are often skipped or rushed through, but they’re the most important part of solving transient circuit problems. Without them, all your differential equations are just guesses.
By getting familiar with how to handle capacitors and inductors at switching moments, you unlock the full power of transient analysis.

Leave a Reply