Real and Reactive Power in 3-Phase AC Systems: A Practical Guide

If you’re working with 3-phase power systems—whether you’re an engineer, technician, or student—understanding how to calculate real (active) and reactive power is essential. It’s not just about crunching numbers. It’s about knowing what those numbers mean in real-world equipment, motors, and power networks.

In this post, we’ll walk through:

• What real and reactive power are,
• Key formulas for 3-phase systems (both balanced and unbalanced),
• And of course, three practical problems—ranging from beginner to advanced—with full solutions.

Let’s dive in.

What Is Real Power?

Real power (also called active power, true power, or simply P) is the power that actually does useful work—like turning motors, lighting bulbs, or running compressors.

It’s measured in watts (W), usually in kilowatts (kW) for industrial systems.

For a balanced 3-phase system:

What Is Reactive Power?

Reactive power (Q) doesn’t do any “real” work, but it’s essential in systems with inductance or capacitance. It maintains electric and magnetic fields in motors, transformers, etc.

It’s measured in VAR (Volt-Ampere Reactive), usually in kVAR.

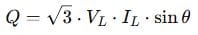
What Is Apparent Power?

Apparent power (S) is the vector sum of real and reactive power. It’s the total power “supplied” to the system, measured in VA or kVA.

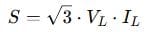
And from power triangle relations:

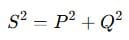
Power Factor: Why It Matters

Power Factor (PF) is the ratio of real power to apparent power:

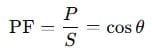
A PF close to 1 means your system is efficient. A low PF means you’re wasting energy with reactive components.

🟢 Beginner Example: Basic Real Power Calculation

Problem:
A 3-phase motor operates at 400 V (line-to-line), draws 10 A of current, and has a power factor of 0.9. What is the real power consumed?

Solution:

We use the real power formula:

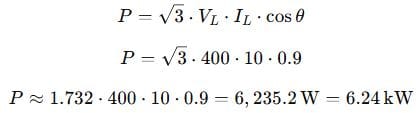
✅ Answer: 6.24 kW

🟡 Intermediate Example: Find Reactive Power

Problem:
The same motor in the previous problem is running at a PF of 0.9. What is the reactive power drawn?

Solution:

First, we find the phase angle:

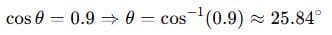
Then calculate:

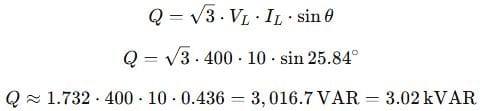
✅ Answer: 3.02 kVAR

🔴 Advanced Example: Power Triangle and Missing Quantity

Problem:
A 3-phase system delivers 15 kW of real power and 20 kVA of apparent power. Find the:

1. Reactive power
2. Power factor
3. Phase angle

Solution:

We use the power triangle relation:

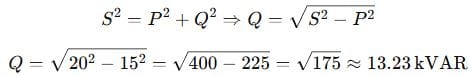
Next, calculate power factor:

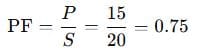
Phase angle:

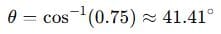
✅ Answers:

1. Reactive Power = 13.23 kVAR
2. Power Factor = 0.75
3. Phase Angle = 41.41°

Additional Notes: Wye vs Delta in Power Calculations

In 3-phase systems, power calculation formulas differ slightly depending on whether you’re dealing with wye (Y) or delta (Δ) configurations:

• In wye, line voltage is √3 × phase voltage, but line current = phase current.
• In delta, line voltage = phase voltage, but line current is √3 × phase current.

Despite these internal differences, the total power calculation for balanced loads is still:

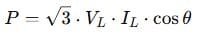
So unless you’re calculating per-phase power or dealing with unbalanced loads, you can use the same formula.

Final Thoughts

Understanding real and reactive power is fundamental for anyone dealing with power systems. Whether you’re sizing a transformer, adjusting power factor, or troubleshooting an overloaded motor, knowing how to compute P, Q, and S gives you a serious edge.

Let’s recap:

• Real power = actual work done
• Reactive power = power stored and released
• Apparent power = total supplied power
• Power factor ties them all together

And most importantly, these values aren’t just theory—they translate directly into efficiency, cost, and equipment life in the real world.

Line and Phase Voltage: Simple Guide for Engineers

Powering Up with Delta and Wye: What You Need to Know