If you’ve ever flipped a switch in a circuit and watched a capacitor voltage creep up (or fall) on your scope, you’ve already met the classic RC charge/discharge curve. In this post, we’ll walk through what actually happens the instant you “switch,” why the waveforms look exponential, how to reason with the time constant τ=RC, and how to quickly size components or estimate delays without grinding through calculus every time. I’ll keep the tone conversational, but we’ll stay technically sharp. At the end you’ll find three fully worked problems (beginner, intermediate, and advanced) you can use to test yourself.
1. What do we mean by a “switching circuit”?
In most practical cases, “switching” just means the circuit’s topology or excitation changes suddenly at some time t=0. For instance:
- You connect a DC source to an uncharged capacitor through a resistor.
- You disconnect that source and let the capacitor bleed off through a resistor.
- You drive an RC network with a PWM (on/off) waveform and wait for it to settle into a periodic steady state.
- A MOSFET or relay toggles, re-routing current paths.
Every one of these creates a transient response described by a first-order differential equation if you’re looking at a single RC (or RL) network. The solution is an exponential—always.
2. The time constant τ=RC
You’ll hear engineers say “it gets there in about five tau.” That “tau” is:
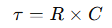
Units: seconds. Physically, τ is the time it takes an RC node to move 63.2% of the way from its initial value to its final value after a step change.
A handy rule of thumb:
- After 1τ: 63.2% of the way to final value
- After 3τ: 95.0%
- After 5τ: 99.3% (engineers often call that “done”)
3. The universal RC step-response formula
Whether you’re charging or discharging, the capacitor voltage obeys this compact expression:
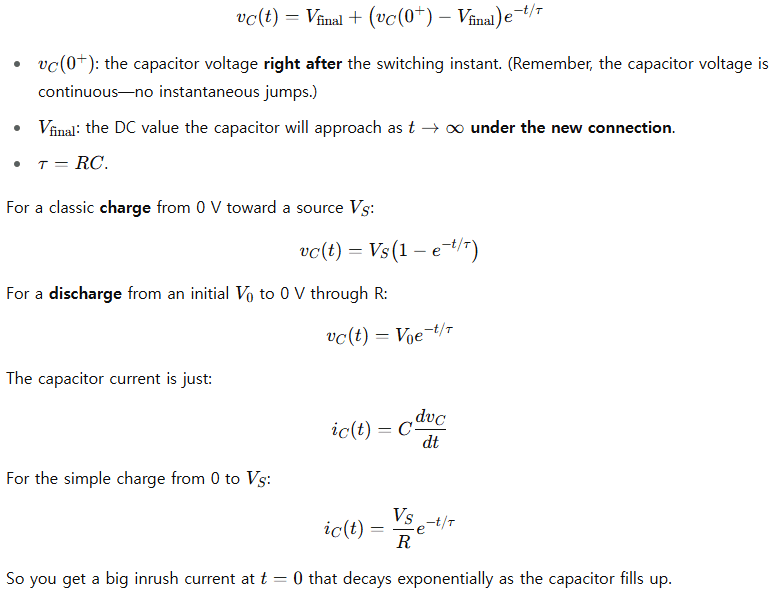
4. Initial and final conditions: the fastest way to solve first-order transients
Instead of re-deriving differential equations every time, memorize the initial/final value + time constant trick:

5. Energy in the capacitor (useful for power and sizing)
Sometimes you care about how much energy you’re dumping into or out of the capacitor. That’s:
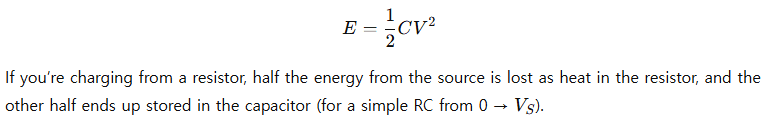
6. Practical rules of thumb you’ll actually use

7. Beginner → Advanced: Three worked examples
Example 1 (Beginner): Simple RC charge
Problem

Example 2 (Intermediate): Discharge to a threshold
Problem
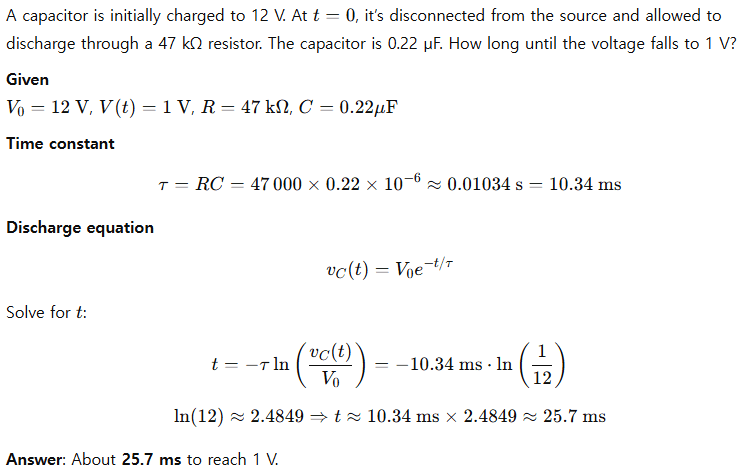
Example 3 (Advanced): Periodic steady-state under PWM
Problem
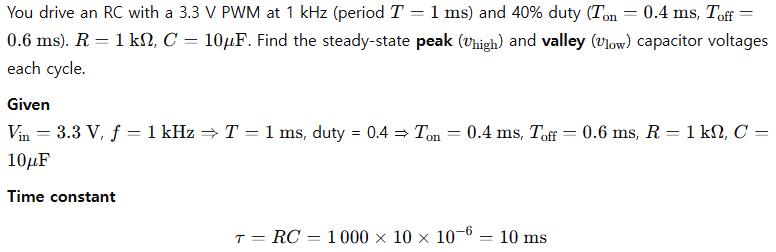
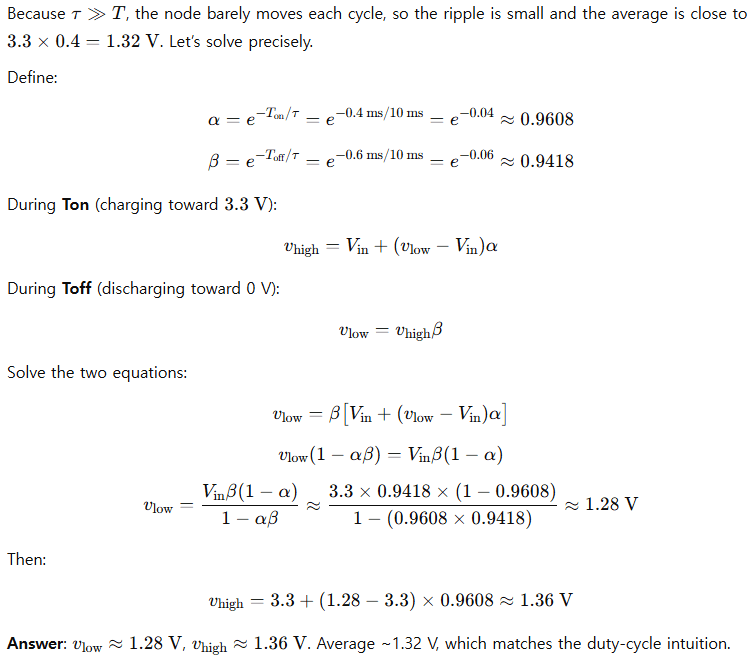
8. Quick design checklist

9. Common pitfalls
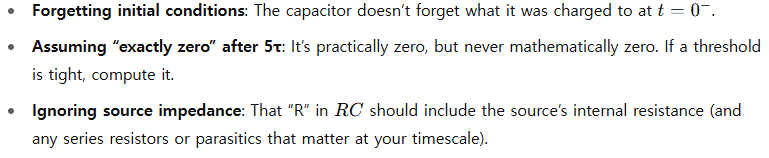
10. Wrap-up


Leave a Reply