1. Power Distribution: Voltage Drop in Long Conductors
In low-voltage DC or high-power AC distribution, voltage drop due to wire resistance becomes critical — especially in long-distance wiring, such as in data centers, battery banks, or solar arrays.
Let’s consider a copper cable delivering DC power to a remote load. The voltage drop across the cable can be calculated using Ohm’s Law:
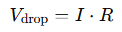
Where R is the total resistance of the conductor (round-trip), which can be derived from its physical properties:

By combining the two equations, we get:
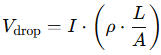
In critical systems, this voltage drop must be minimized to avoid under-voltage faults or energy loss. Engineers use this relationship to size conductors properly and ensure power delivery within regulation limits.
2. Ohm’s Law in Frequency-Domain Analysis
When working with AC signals, especially at high frequencies, simple resistance is no longer sufficient. Ohm’s Law is extended into the complex domain using phasors and impedance.
The frequency-domain version of Ohm’s Law becomes:

For example, in an RLC series circuit:
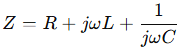
This version allows engineers to analyze magnitude and phase shift of signals, essential in filter design, impedance matching, and resonance analysis.
Ohm’s Law becomes the gateway to powerful AC analysis tools such as:
- Bode plots
- Nyquist diagrams
- S-parameters in RF engineering
3. Thermal-Aware Design Using Ohm’s Law
In power electronics and PCB design, heat is a major constraint. Because resistive power dissipation leads to thermal stress, Ohm’s Law is often used alongside the power formula:
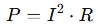
This tells us that even small resistances in traces, vias, or connectors can generate significant heat when current is high.
Now, to model the thermal impact, engineers convert electrical dissipation into thermal rise using thermal resistance:

By using Ohm’s Law to find I or R, and then applying this to thermal equations, one can predict hot spots, optimize copper widths, or even prevent derating of MOSFETs, ICs, or LEDs.
4. Precision Analog Circuits and Error Modeling
In precision analog systems — like instrumentation amplifiers or sensor interfaces — even minor voltage drops due to parasitic resistance can introduce measurement errors.
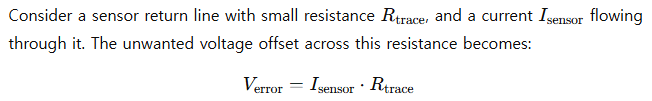
This voltage is added to or subtracted from the actual signal, depending on grounding schemes.
Advanced circuit designers minimize this by:
- Using Kelvin (4-wire) connections
- Selecting low-resistance PCB materials
- Performing common-mode rejection optimization
Even at millivolt levels, Ohm’s Law allows us to quantify and correct for voltage deviation caused by real-world physical effects.
5. High-Speed PCB Design and Transmission Line Effects
In high-speed digital design (e.g., DDR, PCIe, USB 3.x), PCB traces are no longer just “wires” — they behave like transmission lines. At these frequencies, Ohm’s Law is applied through the concept of characteristic impedance:

Matching this impedance with source/load termination is essential to prevent reflections, ringing, and signal distortion.
Although this feels distant from V=IR, at its core, voltage reflection occurs when Ohm’s Law is violated due to impedance mismatch at high speeds.
6. Grounding and Shielding Strategies Based on Resistance
In systems prone to noise, engineers apply Ohm’s Law not just for signal paths, but for ground loops and shield return paths.
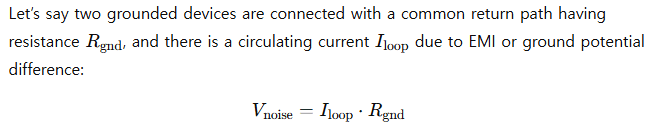
This noise voltage can interfere with sensitive analog signals or create functional instability.
Designers mitigate this by:

Again, Ohm’s Law plays a key role in quantifying how current flow over resistance generates unwanted voltages in unintended places.
Summary: Ohm’s Law as a Design Framework
To advanced engineers, Ohm’s Law is not just a formula — it’s a universal design lens. Whether modeling power loss, analyzing signal integrity, managing thermal behavior, or designing RF systems, the basic relation:
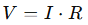
… and its derived forms are used every day — embedded in simulations, calculations, and even design intuition.
Understanding when and how it applies, as well as when it breaks down, is what distinguishes expert-level practice from novice-level learning.
Ohm’s Law Made Easy: An Advanced-Level Guide

Leave a Reply