Mastering Impedance and Admittance: A Beginner’s Guide
In the world of AC circuits, two terms pop up constantly: impedance (Z) and admittance (Y). If you’re dealing with sinusoidal signals, complex numbers, or frequency-dependent components, understanding these concepts is not just helpful—it’s essential.
Let’s break it all down in a conversational way and get you comfortable with how impedance and admittance work, how to calculate them, and why they’re crucial in real-world electrical and electronic systems.
What Is Impedance (Z)?
Impedance is the total opposition a circuit offers to the flow of alternating current (AC). It’s kind of like resistance, but more advanced. Why? Because it accounts for both resistance (R) and reactance (X)—which includes the effects of capacitors and inductors.
Impedance is represented by the symbol Z, and it’s a complex number, written as:

Reactance can be either positive (from inductors) or negative (from capacitors).
For example:
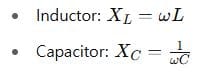
Where:
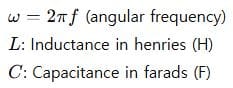
What Is Admittance (Y)?
Admittance is the inverse of impedance. Instead of measuring how much a circuit resists current, admittance tells you how easily it allows current to flow.
It’s represented as:
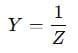
And also written as a complex number:

Admittance is super useful when dealing with parallel circuits. In fact, many circuit problems become easier if you flip everything into admittances instead of using impedances.
Why Use Complex Numbers?
Because voltage and current in AC circuits are sinusoids, and sinusoids are well-handled using phasors and Euler’s formula. Complex numbers let us represent magnitude and phase in one simple term. So yeah—it’s math magic for engineers.
How to Convert Between Z and Y
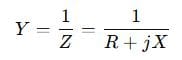
To simplify this, multiply numerator and denominator by the complex conjugate:
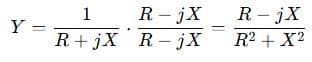
So,
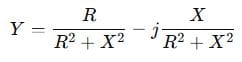
That gives you the real and imaginary parts of admittance.
Example 1: (Beginner Level)
Find the impedance of a 10 Ω resistor in series with a 20 mH inductor at 60 Hz.
Step 1: Find Reactance
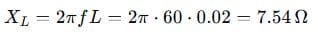
Step 2: Write Impedance
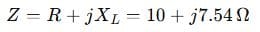
Example 2: (Intermediate Level)
A capacitor of 10 μF is in series with a resistor of 100 Ω. What is the impedance at 50 Hz? Also, find the corresponding admittance.
Step 1: Calculate Capacitive Reactance
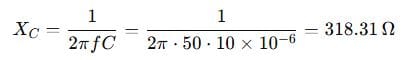
Step 2: Impedance
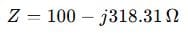
Step 3: Admittance
Use complex conjugate:
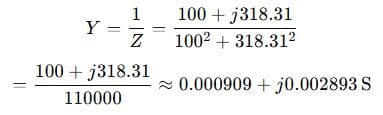
Example 3: (Advanced Level)
You have a parallel RLC circuit with:
- R = 200 Ω
- L = 100 mH
- C = 20 μF
- Frequency = 1 kHz
Find the total admittance of the circuit.
Step 1: Compute individual admittances
Resistor:
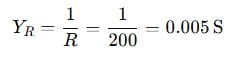
Inductor:
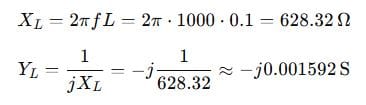
Capacitor:
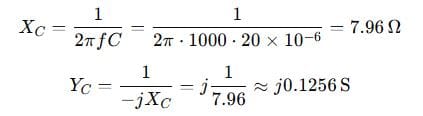
Step 2: Add them up
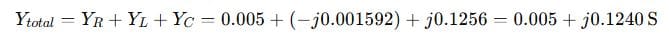
Final Thoughts
Impedance and admittance are more than just fancy words. They let you understand, calculate, and design real-world AC systems—whether it’s power distribution, filters, RF circuits, or audio amplifiers.
When dealing with series circuits, think impedance.
When dealing with parallel circuits, think admittance.
And always remember:
Impedance resists. Admittance permits.
Got it? Good. Now you’re one step closer to mastering AC circuit analysis.
If you want a follow-up post on resonance, Q factor, or impedance matching, let me know!

Leave a Reply