Understanding Sinusoids and Phasor Analysis Made Simple
When you’re working with AC circuits, especially those involving steady-state signals, you’ll quickly find yourself surrounded by sinusoids. They’re everywhere in electrical engineering — voltages, currents, signals. But working directly with time-domain sinusoids can be clunky and difficult. That’s where phasor analysis comes in to save the day.
In this post, we’ll walk through what sinusoids really are, how to express them mathematically, how phasors simplify the math, and how to apply phasor analysis through some hands-on examples.
What Is a Sinusoid?
A sinusoidal function is a smooth periodic oscillation. The general form of a voltage or current sinusoid is:
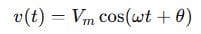
Where:

The Concept of a Phasor
A phasor is a complex number that represents a sinusoid’s magnitude and phase — but not its frequency or time-dependence.
We define a phasor as:
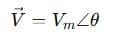
This tells us the amplitude and phase. When we write it in exponential form using Euler’s identity:
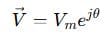
It allows us to work in the frequency domain instead of the time domain. This change makes circuit analysis (especially with impedance) much easier.
From Sinusoid to Phasor
Let’s take an example sinusoidal voltage:
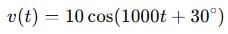
Its phasor representation is:
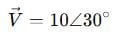
Here, we’ve dropped the time and frequency info because they’re assumed to be the same for all signals in the system. That’s what makes phasor analysis powerful — only phase and magnitude need to be tracked.
To return to the time domain, we apply:
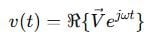
Using Phasors in Circuit Analysis
In AC circuits, components have impedance instead of resistance. Here’s a quick summary:
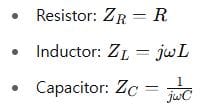
We can now use Ohm’s Law in phasor form:
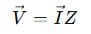
Once everything is converted into phasors and impedances, we solve circuits as if they were DC, and convert the answer back to time domain at the end.
🧠 Example Problems with Solutions
🟢 Beginner Level
Problem 1:
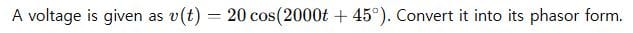
Solution:
Just extract the amplitude and phase:
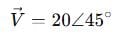
That’s the phasor form. Done.
🟡 Intermediate Level
Problem 2:
Given a circuit with an AC source
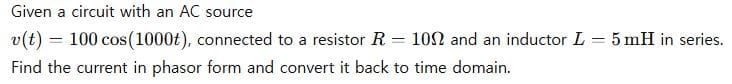
Solution:
Step 1: Convert source to phasor
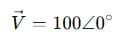
Step 2: Calculate impedance
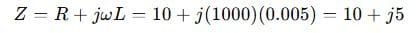
Step 3: Calculate current
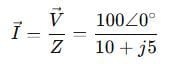
Convert the denominator to polar form:
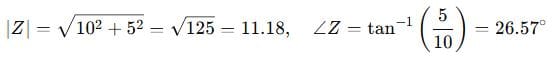
So:
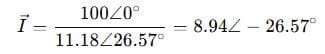
Step 4: Convert to time-domain
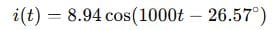
🔴 Advanced Level
Problem 3:

Find total current drawn by the circuit and express it in time domain.
Solution:
Step 1: Source phasor
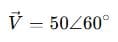
Step 2: Component impedances
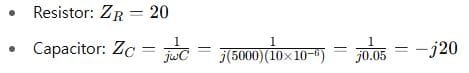
Step 3: Find individual branch currents
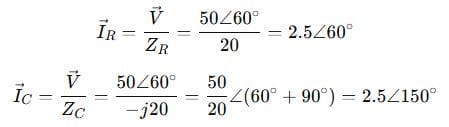
Step 4: Add phasor currents
Convert to rectangular form:
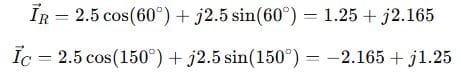
Total current:
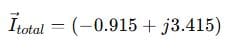
Magnitude:
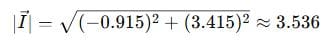
Phase:
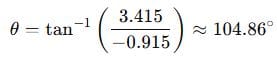
Step 5: Time-domain current
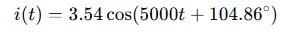
Final Thoughts
Phasor analysis might seem abstract at first, but once you get the hang of it, it radically simplifies the analysis of AC circuits. Instead of juggling trig identities and derivatives, you work with vectors and algebra. It’s a powerful shortcut that every engineer should master.
Whether you’re just starting out or working on more advanced circuits, practicing with phasors will sharpen your understanding and make your AC analysis workflow much faster.

Leave a Reply