Mastering Y-Δ Transformation with Real Examples and Formulas
If you’ve ever scratched your head looking at a complex resistor network or a three-phase system in power electronics, you’re not alone. One of the most useful tools to simplify such networks is the Y-Δ transformation, also known as Delta-Wye or Wye-Delta conversion. Whether you’re dealing with circuits or power systems, mastering this transformation will give you a solid edge in circuit analysis.
In this post, we’re going to break it all down step by step, with explanations, formulas, and three worked-out examples—one easy, one intermediate, and one more advanced.
What is Y-Δ (Delta-Wye) Transformation?
Before jumping into math, let’s get a basic idea. In electrical networks, sometimes you’ll encounter three resistors (or impedances) connected in a triangle—this is the Delta (Δ) configuration. Other times, they’ll be connected like a Y or star—this is the Wye (Y) configuration.
Now, why would we want to convert between these two?
- Simplification. Some complex resistor or impedance networks become way easier to solve once converted.
- Three-phase systems. Electrical engineers deal with Y and Δ connections all the time in motors, transformers, and transmission lines.
When to Use Y-Δ Transformation?
You typically use it when:
- You need to reduce a circuit that isn’t purely in series or parallel.
- You’re analyzing unbalanced three-phase systems.
- You’re working on mesh or nodal analysis where one configuration gives simpler equations.
The Formulas
Δ to Y (Delta to Wye)

Y to Δ (Wye to Delta)
Alternatively, the simpler common formula is:
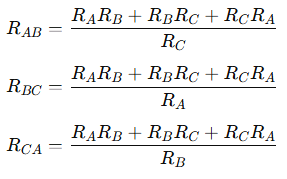
Example 1: Beginner Level (Δ to Y)
Problem:
You are given a Delta configuration with:
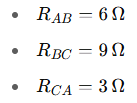
Convert it to an equivalent Y configuration.
Solution:
Total sum of Delta resistors:
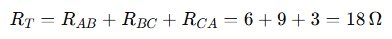
Now calculate each Wye resistor:
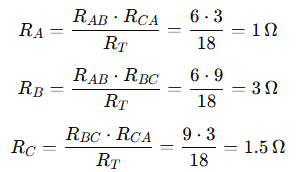
Answer:
The equivalent Y configuration has:
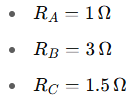
Example 2: Intermediate Level (Y to Δ)
Problem:
Given a Wye network with:
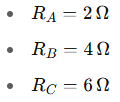
Convert this into a Delta configuration.
Solution:
First calculate the numerator:
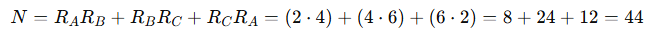
Now compute each Delta resistor:
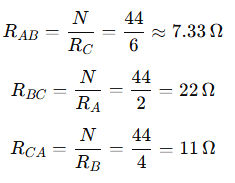
Answer:
The equivalent Δ configuration has:
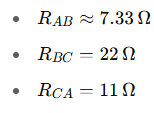
Example 3: Advanced Level – Mixed Circuit Simplification
Problem:
A circuit has a Delta network with:
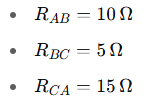
Each node A, B, and C is connected to a 2 Ω resistor which then connects to ground. Find the equivalent resistance between node A and ground.
Solution:
Step 1: Convert Δ to Y
Total resistance:
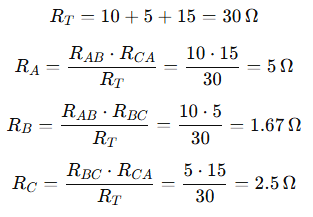
Step 2: Add Series Resistors to Ground
Now at each node, we have:
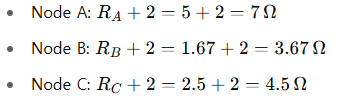
Step 3: Find Equivalent Resistance from A to Ground
Now, we look from node A into the circuit. Node A is connected to center of Y. This point is also connected to B and C branches.
We now have:
- One 7 Ω resistor from A to the center
- Then from the center to ground via two parallel resistors: 3.67 Ω and 4.5 Ω
Parallel part:
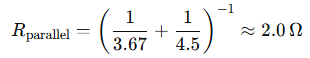
Total resistance:
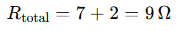
Answer:
The total resistance from node A to ground is approximately 9 Ω
Final Thoughts
Y-Δ transformation isn’t just academic—it’s a powerful real-world tool that every electrical engineer, technician, or even hobbyist should have in their mental toolbox. Once you get comfortable with the formulas and recognize patterns in circuits, you’ll find many problems that once seemed complicated become far more manageable.
Try using this on homework problems, three-phase analysis, or resistor simplification questions—you’ll be amazed how much easier life becomes!
If you found this helpful, consider bookmarking this post or sharing it with fellow engineers. Want more deep dives like this? Let me know what you’d like to see next!

Leave a Reply