What is Reactive Current?

Let’s be honest—when you first heard “reactive current,” you probably asked, “Is this just another confusing concept in AC circuits?” Well, yes and no. While it might seem intimidating, it’s actually one of the most practical ideas you’ll use in electrical engineering and power systems.

Let’s break it down in plain English.

The Basics: Reactive vs. Active Current

In AC (alternating current) circuits, not all current is used to do useful work. Some of it is just “moving back and forth” without actually powering anything. That’s where the idea of reactive current comes in.

• Active current (Iₐ) is the part of the current that does real work—like lighting a bulb or running a motor.
• Reactive current (Iᵣ) is the part of the current that doesn’t do real work but supports magnetic or electric fields, especially in inductors and capacitors.

The total current (I) in an AC system is made up of both:

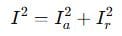
That’s the current version of the Pythagorean theorem!

Why Does Reactive Current Matter?

Reactive current doesn’t consume real power (watts), but it does affect your system. It can cause:

• Increased losses in the transmission lines
• Overheating in transformers
• Reduced efficiency in power delivery
• Higher electricity bills if power factor is low

Power companies don’t like poor power factor. And reactive current is the main culprit behind it.

Reactive Current and Power Triangle

We often use the power triangle to visualize how real power (P), reactive power (Q), and apparent power (S) interact.

Where:

• Q is reactive power (VAR)
• V is voltage (RMS)
• Iᵣ is reactive current (RMS)

The Role of Inductors and Capacitors

• Inductors (like motors, transformers) cause current to lag behind voltage. They generate positive reactive power.
• Capacitors cause current to lead voltage. They generate negative reactive power.

So, depending on the device, reactive current can either be lagging or leading.

Real-World Example: Power Factor Correction

Let’s say a factory uses a lot of motors (inductive loads), so their power factor drops to 0.7. They install capacitor banks to supply negative reactive current, which cancels out some of the lagging reactive current from the motors.

This raises the power factor to 0.95, reducing their total current and electricity bill. Win-win.

🔹 Beginner Level

Problem:
An AC load consumes 100 W of real power and 75 VAR of reactive power. Find the reactive current if the RMS voltage is 100 V.

Solution:

We know:

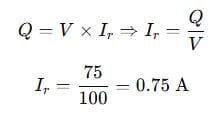
✅ Answer: 0.75 A

🔹 Intermediate Level

Problem:
An AC circuit has a total current of 5 A. The active current is 4 A. Find the reactive current and the power factor.

Solution:

Using Pythagoras:

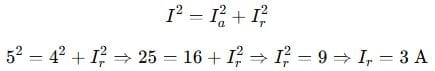
Now, power factor:

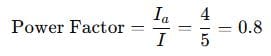
✅ Answer: Reactive Current = 3 A, Power Factor = 0.8

🔹 Advanced Level

Problem:
A motor runs at 220 V RMS and draws 10 A RMS with a power factor of 0.6 lagging. Calculate:
(a) Real power (P),
(b) Reactive power (Q),
(c) Reactive current (Iᵣ)

Solution:

(a) Real Power:

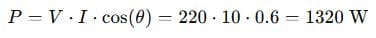
(b) Apparent Power:

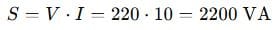
Now use the power triangle:

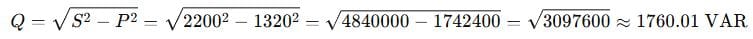
(c) Reactive Current:

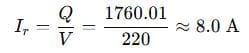
✅ Answer: P = 1320 W, Q ≈ 1760 VAR, Iᵣ ≈ 8.0 A

Final Thoughts

Reactive current isn’t “bad,” but too much of it creates inefficiencies. Managing it—using capacitors, improving power factor, and understanding your load—is key to efficient energy use in industrial and commercial settings.

Whether you’re a student, engineer, or someone curious about how the electric grid works, mastering reactive current will help you design better, smarter systems.

Mastering RMS Current: How to Calculate and Understand