When we talk about alternating current (AC), the values we see aren’t always as straightforward as those in direct current (DC) systems. One of the most important concepts in AC circuits is RMS current—or Root Mean Square current. But what exactly is it? Why do we use it? And how can you calculate it in real-world scenarios?

Let’s dive in, step-by-step.

🔌 What Is RMS Current?

RMS stands for Root Mean Square. It might sound complicated, but the idea is actually simple: RMS current is the equivalent DC current that would produce the same heating effect in a resistor as the AC current.

In AC, current and voltage vary over time—typically in a sinusoidal form. Since the current isn’t constant, we can’t just use the average value (which is zero in pure sine waves). Instead, we use the RMS value, which gives us a meaningful measure of power delivery.

🧮 RMS Current Formula for Sinusoidal Waveforms

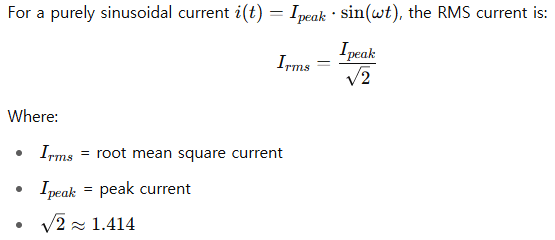
This formula works only for sine waves. If the waveform is non-sinusoidal, you’ll need to use integration or summation methods, which we’ll get into later.

⚡ Why RMS Current Matters

Think of a simple heater or toaster. What matters to that device is how much energy (heat) it receives. RMS current directly tells us how much heating power is being delivered. That’s why electrical ratings on appliances and circuit breakers are typically given in RMS values.

So when your multimeter shows “5A AC,” it means 5A RMS, not peak.

🔍 More General RMS Definition

In general, RMS current is defined as:

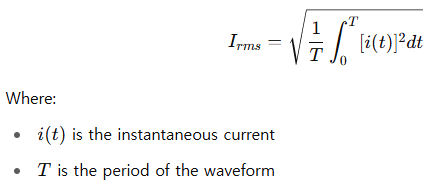
This integral squares the current (to eliminate sign), averages it, then takes the square root. That’s the “Root Mean Square” process.

📉 RMS Current for Other Waveforms

Let’s quickly look at RMS current for a few common waveforms:

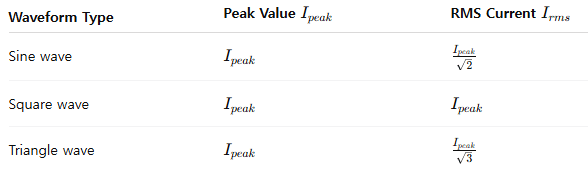
✅ Beginner Level

Problem:
A sinusoidal current has a peak value of 10 A. What is the RMS current?

Solution:
We use the standard formula:

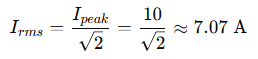
Answer:
The RMS current is approximately 7.07 A.

✅ Intermediate Level

Problem:
An AC circuit has an RMS current of 5 A flowing through a 20-ohm resistor. What is the average power dissipated?

Solution:
Use the power formula with RMS current:

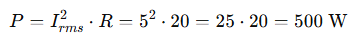
Answer:
The average power dissipated is 500 watts.

✅ Advanced Level

Problem:
A non-sinusoidal current waveform over one period is defined as:

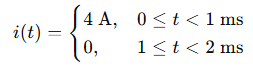
and this pattern repeats every 2 milliseconds. Calculate the RMS current.

Solution:
We apply the general RMS definition:

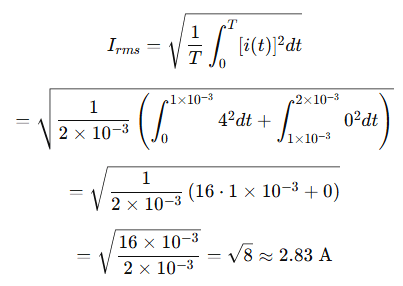
Answer:
The RMS current is approximately 2.83 A.

🔧 Practical Tip

If you’re using a multimeter to measure AC current, check if it’s a True RMS meter. Many cheap meters only give correct readings for sine waves—not for distorted waveforms. In power electronics or PWM circuits, a True RMS meter is a must.

🧠 Final Thoughts

RMS current is not just a theoretical concept—it’s a practical necessity in AC systems. It helps engineers, electricians, and even students understand how much “real” power is flowing, and it’s the standard for comparing electrical loads. Whether you’re sizing a fuse, designing a power supply, or just reading your multimeter, knowing what RMS current means gives you real insight into the energy in your circuit.