In the expansive world of electrical engineering, few laws have endured the test of time and technological change like Kirchhoff’s Voltage Law, commonly known as KVL. At first glance, KVL may appear deceptively simple — the idea that the sum of all voltages around a closed loop is zero. But beneath its straightforward exterior lies one of the most powerful tools for analyzing, modeling, and understanding the behavior of electrical circuits.
Whether you’re designing complex communication hardware, troubleshooting a faulty sensor circuit, or studying for an electrical engineering exam, mastering KVL is absolutely essential. It not only offers foundational insight into how voltage behaves in a loop, but also serves as the stepping stone for more advanced analysis techniques such as mesh analysis, state-space modeling, and Laplace-domain transformations.
Despite being introduced early in most circuit theory courses, KVL is far from a “beginner-only” concept. It remains central to modern engineering practices and is used extensively in real-world applications, from microcontroller-based embedded systems to power transmission networks. Even as circuit designs become more integrated and systems more software-driven, the need to understand and apply KVL remains critical — because every complex system is built on simpler principles, and KVL is one of the most fundamental.
Practical Utility Across All Levels of Engineering
From the simplest flashlight to a complex multilayer PCB used in aerospace systems, circuits are governed by the same set of physical laws. Among these, KVL is indispensable.
Here are just a few examples of where KVL plays a critical role:
- Power supply design: Ensuring proper voltage regulation and dropout margins
- Operational amplifier circuits: Predicting output swing based on loop voltage drops
- Filter networks: Analyzing voltage behavior across RLC components
- Fault analysis: Determining open/short conditions through abnormal voltage behavior
- AC signal processing: Applying KVL in the phasor domain with complex impedances
- Embedded system design: Validating low-power rail distributions in MCU-based boards
As you progress through your career or studies in electrical engineering, you’ll find yourself coming back to KVL time and time again.
Example 1: Simple Series Circuit
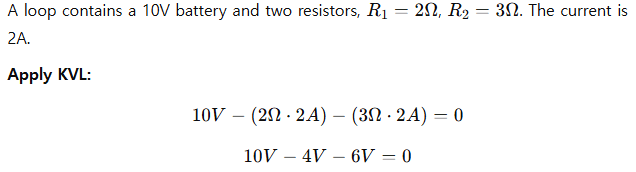
Example 2: Series Circuit with Unknown Voltage
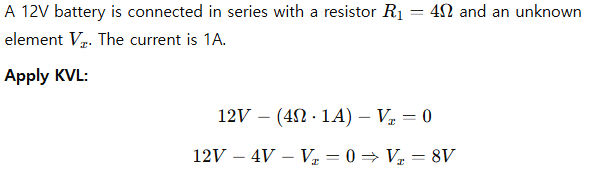
Example 3: Loop with Voltage Rise and Drop
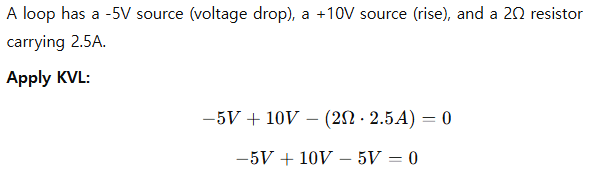
Example 4: Loop with Three Resistors

Example 5: Opposing Voltage Sources

Example 6: Loop with Unknown Current

Example 7: Two Loops Sharing One Resistor
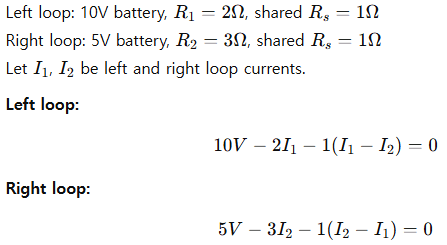
Example 8: AC Loop with Impedance
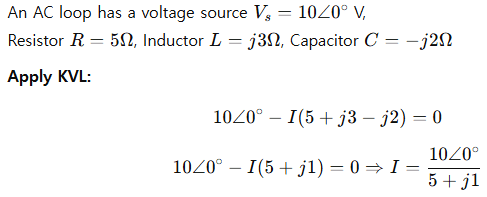
Example 9: KVL with a Diode
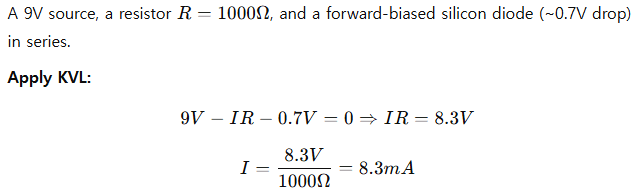
Example 10: Loop with Dependent Source
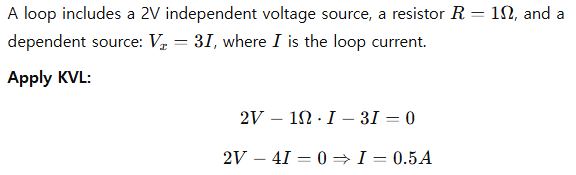
Beyond Theory: Why Examples Matter
If you’ve learned KVL only through lecture notes or textbook explanations, you might have developed a theoretical understanding — but not necessarily an intuitive one. Like many areas in engineering, circuit analysis is best learned through practice, especially with progressively challenging examples.
When you work through real-world circuits, each with their own sources, resistive elements, reactive components, or dependent variables, you start to develop a much deeper sense of how voltages interact. You learn to recognize patterns. You learn to predict behavior. And most importantly, you gain confidence.
For instance:
- How does a shared resistor behave in two interconnected loops?
- How do voltage signs flip depending on current direction?
- What happens to KVL when a loop contains an active or dependent source?
- How does KVL behave in frequency-domain analysis with phasors?
These aren’t questions a formula sheet can answer. They’re insights earned by solving real examples — and that’s exactly what this post provides.
Kirchhoff’s Voltage Law made Easy: A Beginner’s Guide

Leave a Reply