지수응답과 임펄스응답이 중요한 이유
전기회로 해석에서 가장 중요한 개념 중 하나는 시스템의 응답입니다. 특히, 시간 영역 해석을 다룰 때는 입력에 따라 시스템이 어떻게 반응하는지를 아는 것이 핵심입니다. 그중 지수응답(Exponential Response)과 임펄스응답(Impulse Response)은 일시적인 과도현상을 설명하는 데 있어 매우 중요한 역할을 합니다.
지수응답은 보통 전류나 전압이 시간이 지남에 따라 어떤 식으로 변하는지를 나타내며, 특히 일차 또는 이차 시스템의 응답 형태를 기술할 때 필수적입니다. 반면, 임펄스응답은 단위 임펄스 함수에 대한 시스템의 출력으로, 시스템의 전반적인 특성을 완전히 파악할 수 있게 해줍니다.
1. 지수응답의 기본 개념
지수응답은 일반적으로 다음과 같은 형태를 가집니다:
여기서,
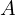는 초기 크기,
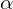는 감쇠 상수,
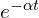는 시간이 지남에 따라 감쇠되는 특성을 나타냅니다.
이 함수는 
일 때 
으로 수렴하는, 즉 안정된 시스템의 전형적인 예입니다.
지수응답의 실제 예: 일차 RL 회로
다음은 간단한 RL 직렬 회로에서의 지수응답 예시입니다.
- 전압원:
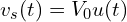
- 저항:
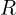
- 인덕터:
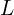
회로 방정식은 다음과 같이 주어집니다:
이를 풀면 다음과 같은 지수 응답을 얻을 수 있습니다:
이 식은 전류가 시간이 지남에 따라 
로 수렴함을 보여줍니다. 이는 인덕터가 처음에는 전류의 변화를 방해하다가 점차 전류를 허용하게 되는 물리적 의미를 갖습니다.
2. 임펄스응답이란 무엇인가?
임펄스응답은 시스템에 단위 임펄스 
를 가했을 때 출력되는 함수입니다. 시스템의 선형성 및 시불변성을 가정할 경우, 임펄스응답만 알면 임의의 입력에 대한 응답을 컨볼루션을 통해 구할 수 있습니다.
여기서 
는 임펄스응답입니다.
3. 임펄스응답의 예: RC 회로
RC 직렬회로에서 임펄스응답을 구해보겠습니다.
- 저항:
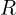
- 커패시터:
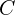
- 입력:
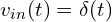
시스템의 미분방정식은 다음과 같습니다:
라플라스 변환을 이용하면 다음과 같은 전달함수를 구할 수 있습니다:
임펄스응답은 역라플라스 변환을 통해 다음과 같이 됩니다:
이는 지수적으로 감쇠하는 응답으로, 시스템이 임펄스 입력에 어떻게 반응하는지를 보여줍니다.
4. 지수응답과 임펄스응답의 관계
임펄스응답은 사실 시스템의 고유한 특성을 나타내며, 지수응답 역시 시스템의 차수 및 특성에 따라 임펄스응답과 비슷한 형태를 띨 수 있습니다.
예를 들어, 일차 시스템의 임펄스응답은 지수함수로 나타나고, 이차 시스템의 경우에는 감쇠진동 형태의 지수함수를 포함하게 됩니다.
이런 식으로, 다양한 형태의 지수함수들이 임펄스응답의 구성요소로 포함될 수 있습니다.
5. 그래프로 보는 응답
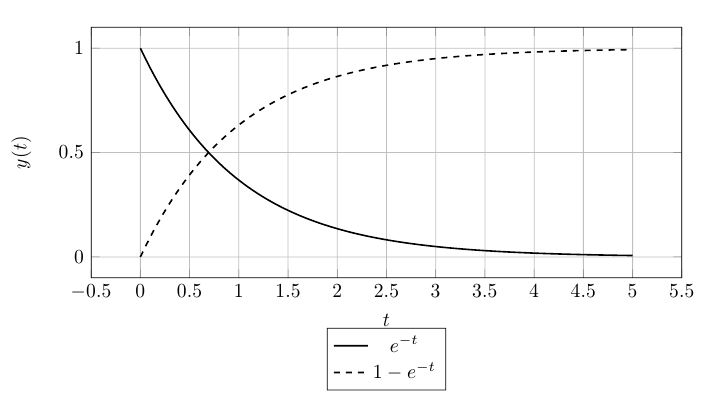
6. 응답을 계산하는 방법 요약
| 구분 | 방식 | 대표 수식 |
|---|---|---|
| 지수응답 | 미분방정식 해법 |  |
| 임펄스응답 | 전달함수의 역라플라스 |  |
| 시스템 출력 | 컨볼루션 |  |
7. 마무리: 실무에서의 활용
전자공학, 자동제어, 통신 등 대부분의 엔지니어링 분야에서 지수응답과 임펄스응답은 시스템의 거동을 예측하고 제어하기 위해 필수적인 도구입니다. 실제 회로 설계 시, 시간 응답을 통해 시스템의 안정성을 분석하고, 제어기의 설계를 최적화합니다.
Leave a Reply