1. 왜 DC vs AC를 구분해야 할까?
현대 전력·전자 시스템은 배터리, 서버, 전기차처럼 ![]() 가 핵심인 영역과, 송배전/산업용 모터처럼
가 핵심인 영역과, 송배전/산업용 모터처럼 ![]() 가 필수인 영역이 공존합니다. 어떤 값을 계산하느냐(예:
가 필수인 영역이 공존합니다. 어떤 값을 계산하느냐(예: ![]() , 위상
, 위상 ![]() ), 어떤 부품을 쓰느냐(정류기, 인버터,
), 어떤 부품을 쓰느냐(정류기, 인버터, ![]() 등), 어떤 안전/규격을 준수하느냐까지 파형의 본질이 모든 의사결정을 좌우합니다.
등), 어떤 안전/규격을 준수하느냐까지 파형의 본질이 모든 의사결정을 좌우합니다.
2. 정의: DC와 AC
- 직류(DC, Direct Current)
시간에 따라 전압/전류의 부호가 바뀌지 않고 평균값이 0이 아니며, 이론적으로 일정합니다. 배터리,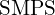 의 출력, 마이크로컨트롤러 전원 등이 대표적입니다. 실제로는 리플(ripple)이 존재하므로,
의 출력, 마이크로컨트롤러 전원 등이 대표적입니다. 실제로는 리플(ripple)이 존재하므로, 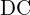 + 리플(사소한
+ 리플(사소한 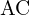 성분)로 보는 것이 실무적입니다.
성분)로 보는 것이 실무적입니다. - 교류(AC, Alternating Current)
시간에 따라 부호가 주기적으로 바뀌며 평균값이 0(또는 특정 기준)인 신호가 전형적입니다. 가장 흔한 경우가 정현파로,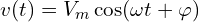
여기서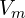 은 최대값(피크),
은 최대값(피크), 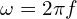 는 각주파수,
는 각주파수, 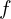 는 주파수(한국은 보통
는 주파수(한국은 보통 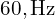 ),
), 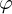 는 위상입니다.
는 위상입니다.
3. 핵심 수치: 피크, RMS, 평균
- RMS(Root Mean Square)
정현파 기준 전압/전류의 실효값은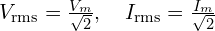
전력(순수 저항 부하) 계산에서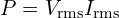 가 바로 유효 전력입니다.
가 바로 유효 전력입니다. - 평균값(정류 후 평균)
반파/전파 정류 시 평균이 0이 아니며, 예를 들어 전파 정류된 정현파의 평균은
![]()
위상(Phase)과 위상차![]() (또는
(또는 ![]() )는 전압과 전류 사이의 시간적 지연을 각도로 표현합니다.
)는 전압과 전류 사이의 시간적 지연을 각도로 표현합니다.
전력 인자(Power Factor, ![]() )는
)는
![]()
4. 전력: 유효전력 P, 무효전력 Q, 피상전력 S
교류 회로에서(특히 유도성/용량성 부하 포함) 전압과 전류는 위상이 어긋납니다. 이때![]()
![]()
![]()
이며,![]()
가 성립합니다.
5. 시간영역 vs. 위상자(Phasor) 영역
정현파 정상상태의 ![]() 해석에서는 위상자(phasor) 표기가 대단히 편리합니다. 예를 들어,
해석에서는 위상자(phasor) 표기가 대단히 편리합니다. 예를 들어,![]()
![]()
와 같이 복소수 형태로 표현하면, 미분/적분 성분(코일 ![]() , 커패시터
, 커패시터 ![]() )이 곱셈/나눗셈으로 바뀌어 회로 해석이 단순화됩니다. 이때 임피던스는
)이 곱셈/나눗셈으로 바뀌어 회로 해석이 단순화됩니다. 이때 임피던스는![]()
![]()
![]()
입니다. 여기서 ![]() 이며,
이며, ![]() 는 각주파수입니다.
는 각주파수입니다.
6. 왜 송배전은 AC, 많은 전자회로는 DC인가?
- 송배전(대규모 전력): 전통적으로
 는 변압기가 간단해 고전압/저전류로 손실을 줄이기 쉬웠습니다. 최근에는
는 변압기가 간단해 고전압/저전류로 손실을 줄이기 쉬웠습니다. 최근에는 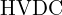 도 장거리/해저 케이블 등에서 효율/제어상의 이점으로 빠르게 확대되고 있습니다(컨버터 비용/복잡도는 증가).
도 장거리/해저 케이블 등에서 효율/제어상의 이점으로 빠르게 확대되고 있습니다(컨버터 비용/복잡도는 증가). - 전자회로(저전력, 디지털): 반도체는 안정된
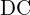 레일이 필요합니다. 그래서
레일이 필요합니다. 그래서 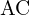 를 받아 정류/평활하여
를 받아 정류/평활하여 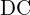 로 변환하고, 필요 시
로 변환하고, 필요 시  로 레일을 쪼개어 배분합니다.
로 레일을 쪼개어 배분합니다.
7. 정류기·인버터·PFC: DC↔AC 변환의 실무
- 정류기(Rectifier):
 . 다이오드 브리지,
. 다이오드 브리지,  ,
,  부스트
부스트  등 다양한 토폴로지가 있습니다. 전파 정류 후 필터를 통해 리플을 줄입니다.
등 다양한 토폴로지가 있습니다. 전파 정류 후 필터를 통해 리플을 줄입니다. - 인버터(Inverter):
 . 스위칭 소자를
. 스위칭 소자를  으로 구동해 원하는 주파수/전압의 정현파 및 모터 구동을 구현합니다. 전압형 인버터(VSI), 전류형 인버터(CSI) 등이 대표적입니다.
으로 구동해 원하는 주파수/전압의 정현파 및 모터 구동을 구현합니다. 전압형 인버터(VSI), 전류형 인버터(CSI) 등이 대표적입니다. - PFC(Power Factor Correction): 전력 인자를 1에 가깝게 만들어 효율적이며 규격 적합한 입력 전류 파형을 만드는 기술입니다.
8. 안전, 노이즈(EMI), 접지
 는 전압이 높고 인덕티브/커패시티브 결합을 통해 노이즈 커플링이 강해질 수 있습니다.
는 전압이 높고 인덕티브/커패시티브 결합을 통해 노이즈 커플링이 강해질 수 있습니다.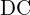 측이라도 스위칭(예:
측이라도 스위칭(예: 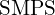 ) 때문에 고주파 성분이 많아 **
) 때문에 고주파 성분이 많아 **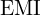 필터링, 레이아웃, 접지(스타 접지/플레인 분리)**가 매우 중요합니다.
필터링, 레이아웃, 접지(스타 접지/플레인 분리)**가 매우 중요합니다.
9. 언제 무엇을 써야 할까? (의사결정 가이드)
- 배터리 기반, 로직/마이컴/센서 → 거의 항상
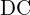
- 대전력 모터, 배전, 변전 → 전통적으로
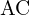 , 단 장거리/특수 구간은
, 단 장거리/특수 구간은 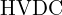
- 가변 속도 드라이브(VFD) →
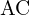 모터지만, 정류-링크-인버터로 내부는
모터지만, 정류-링크-인버터로 내부는 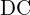 를 경유
를 경유 - 재생에너지(태양광
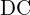 ) ↔ 계통(
) ↔ 계통(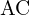 ) 연계 → 인버터/컨버터가 핵심
) 연계 → 인버터/컨버터가 핵심
10. 예제문제 6문제 (초급 2, 중급 2, 고급 2) — 풀이 포함
초급 1
문제: 가정용 정현파 전원 ![]() 일 때, 피크 전압
일 때, 피크 전압 ![]() 은?
은?
해설:
![]()
초급 2
문제: ![]()
![]() 전원을
전원을 ![]() (
(![]() 는
는 ![]() ) 저항에 걸었다. 전류와 순간 전력, 5분 동안 소비된 에너지는?
) 저항에 걸었다. 전류와 순간 전력, 5분 동안 소비된 에너지는?
해설:
전류![]()
전력![]()
에너지
![]()
중급 1
문제: 전파 정류된 정현파의 피크 ![]() 일 때, 평균 전압
일 때, 평균 전압 ![]() 는?
는?
해설:
![]()
중급 2
문제:
![]()
,
![]()
, 전력 인자 ![]() (지상, lagging).
(지상, lagging). ![]() 를 구하라.
를 구하라.
해설:![]()
![]()
![]()
고급 1
문제: ![]() [/latex],
[/latex], ![]() 직렬 회로에
직렬 회로에 ![]()
![]() ,
, ![]() 를 인가.
를 인가. ![]() 와 전류 위상각(전압 기준 지연각)을 구하라.
와 전류 위상각(전압 기준 지연각)을 구하라.
해설:![]()
![]()
![]()
![]()
![]()
위상각(전류가 지연):![]() (전류는
(전류는 ![]() 지연)
지연)
고급 2
문제: ![]() 인 전압형 인버터(VSI)가 변조지수
인 전압형 인버터(VSI)가 변조지수 ![]() 로 단상 정현파를 생성한다. 기저 성분의 최대 피크 전압
로 단상 정현파를 생성한다. 기저 성분의 최대 피크 전압 ![]() 와
와 ![]() (정현파 기준)를 구하라. (단, 단상 반브리지 기준
(정현파 기준)를 구하라. (단, 단상 반브리지 기준 ![]() 가정)
가정)
해설:![]()
![]()
11. 정리(Conclusions)
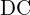 는 안정성, 제어 용이성이,
는 안정성, 제어 용이성이, 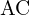 는 송배전 변압·위상 해석의 효율이 강점입니다.
는 송배전 변압·위상 해석의 효율이 강점입니다.- 실무에서는 **양자 간 변환(정류/인버터)**을 전제로 하며,
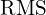 ,
, 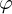 ,
, 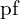 ,
, 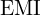 같은 지표가 필수입니다.
같은 지표가 필수입니다. - 고급 해석일수록 위상자(복소수) 해법과 주파수 영역 사고방식이 생산성을 높입니다.

Leave a Reply