Introduction to Electromagnetic Induction
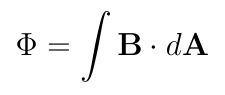
Electromagnetic induction is a fundamental principle in electromagnetism that explains how electric currents can be generated by changing magnetic fields. This phenomenon forms the foundation of many electrical devices, including transformers, electric generators, and inductors.
At the heart of electromagnetic induction are Faraday’s Law and Lenz’s Law, which quantitatively describe how a change in magnetic flux through a circuit induces an electromotive force (emf). Understanding these laws, along with the concept of magnetic flux, is essential for engineers and physicists working in electrical and electronic fields.
Magnetic Flux (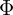 )
)
Magnetic flux (![]() ) measures the quantity of magnetic field lines passing through a surface area. It is analogous to the amount of “magnetic flow” through a loop or coil.
) measures the quantity of magnetic field lines passing through a surface area. It is analogous to the amount of “magnetic flow” through a loop or coil.
Formally, magnetic flux is defined as:
![]()
Where:
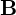 is the magnetic field vector (in Tesla, T),
is the magnetic field vector (in Tesla, T),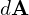 is an infinitesimal area vector perpendicular to the surface (in square meters, m²),
is an infinitesimal area vector perpendicular to the surface (in square meters, m²),- The dot product signifies that only the component of
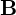 perpendicular to the surface contributes to the flux.
perpendicular to the surface contributes to the flux.
For a uniform magnetic field perpendicular to a flat surface of area ![]() , this simplifies to:
, this simplifies to:
![]()
If the magnetic field is at an angle ![]() to the normal vector of the surface, then:
to the normal vector of the surface, then:
![]()
Magnetic flux is measured in Weber (![]() ), where 1
), where 1 ![]() .
.
Faraday’s Law of Electromagnetic Induction
Faraday’s Law states that a change in magnetic flux through a closed circuit induces an electromotive force (emf) in the circuit. This induced emf drives a current if the circuit is closed.
Mathematically:
![]()
Where:
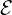 is the induced emf (in volts),
is the induced emf (in volts),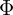 is the magnetic flux through the circuit,
is the magnetic flux through the circuit,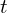 is time.
is time.
The negative sign is critical and relates to Lenz’s Law, which indicates the direction of the induced emf opposes the change in flux causing it.
If the circuit has ![]() turns (loops), the total induced emf is:
turns (loops), the total induced emf is:
![]()
Lenz’s Law
Lenz’s Law provides the direction of the induced current or emf. It states:
The induced current in a closed conducting loop will flow in a direction such that the magnetic field created by the induced current opposes the change in magnetic flux through the loop.
This law ensures the conservation of energy and is represented by the negative sign in Faraday’s Law. Physically, if the magnetic flux increases, the induced current generates a magnetic field opposing the increase; if it decreases, the induced current acts to maintain it.
Induced Electromotive Force (emf) and Current
When the magnetic flux through a conductor changes, an emf is induced, which can cause a current to flow if the conductor forms a closed path.
The magnitude of the induced emf depends on:
- The rate of change of magnetic flux,
- The number of turns in the coil,
- The geometry and orientation of the coil relative to the magnetic field.
Practical Applications
- Electric Generators: Convert mechanical energy into electrical energy by rotating coils in a magnetic field.
- Transformers: Transfer electrical energy between circuits via changing magnetic flux in coils.
- Inductors: Store energy in magnetic fields created by current changes.
Example Problems
Beginner Level
Problem 1:
A single loop of wire with area 0.05 m² is placed perpendicular to a uniform magnetic field of 0.2 T. The magnetic field is reduced to zero uniformly over 0.1 seconds. Calculate the magnitude of the induced emf in the loop.
Solution:
Initial flux:
![]()
Final flux:
![]()
Change in flux:
![]()
Rate of change of flux:
![]()
Induced emf:
![]()
Problem 2:
A coil with 50 turns has an area of 0.01 m² per turn. A magnetic field perpendicular to the coil changes from 0.5 T to 0 T in 0.05 seconds. Calculate the induced emf.
Solution:
Initial flux per turn:
![]()
Final flux:
![]()
Total change in flux for 50 turns:
![]()
Rate of change:
![]()
Induced emf:
![]()
Intermediate Level
Problem 3:
A rectangular coil with dimensions 0.2 m by 0.1 m and 100 turns is rotating with an angular velocity of ![]() in a uniform magnetic field of 0.3 T. Find the maximum induced emf.
in a uniform magnetic field of 0.3 T. Find the maximum induced emf.
Solution:
Maximum flux per turn occurs when the coil is perpendicular to the magnetic field:
![]()
The induced emf varies sinusoidally with time:
![]()
Maximum emf is the amplitude:
![]()
Problem 4:
A coil with 200 turns and an area of 0.02 m² is placed in a magnetic field that changes according to ![]() T. Find the expression for the induced emf as a function of time.
T. Find the expression for the induced emf as a function of time.
Solution:
Magnetic flux:
![]()
Induced emf:
![]()
Advanced Level
Problem 5:
A solenoid with 500 turns and length 0.5 m carries a current increasing at a rate of 2 A/s. The radius of the solenoid is 0.05 m. Find the induced emf in a single loop placed coaxially inside the solenoid, assuming the magnetic field is uniform inside.
Solution:
Magnetic field inside solenoid:
![]()
Where ![]()
Rate of change of magnetic field:
![]()
Area of loop:
![]()
Induced emf in loop:
![]()
Magnitude:
![]()
Problem 6:
A rectangular coil with 200 turns and dimensions 0.3 m by 0.1 m moves at a velocity of 5 m/s out of a region with a uniform magnetic field of 0.6 T. Find the emf induced in the coil if it completely exits the field in 0.02 seconds.
Solution:
Magnetic flux per turn initially:
![]()
Final flux:
![]()
Total flux change:
![]()
Induced emf:
![]()
Conclusion
Electromagnetic induction, governed by Faraday’s and Lenz’s laws, is a cornerstone of modern electrical engineering and physics. The ability to convert mechanical motion or changing magnetic fields into electrical energy underpins the operation of countless devices. Mastery of these principles, including magnetic flux calculation and emf induction, is essential for practical application and innovation.

Leave a Reply