1) So… what exactly is an “electrical machine”?
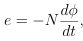
In the most conservative, textbook sense, an electrical machine is any device that converts energy between electrical and non‑electrical domains, or between different electrical forms. Concretely:
- Motors: electrical → mechanical
- Generators: mechanical → electrical
- Transformers: electrical (AC) → electrical (AC), different voltage/current levels (no mechanical shaft)
You’ll also see power‑electronics converters bundled into “electrical machinery” in some curricula, but strictly speaking they’re static semiconductor converters, not classical electromagnetic machines. We’ll keep our scope to the classical trio above.
2) Core physical laws (why machines work)
All rotating electrical machines and transformers ultimately rely on two pillars:
- Faraday’s law of induction (voltage from changing flux)
![]()
Lorentz force / Ampère’s law (force/torque from current in a magnetic field)
![]()
For sinusoidal AC machines (and transformers), the RMS induced EMF per phase is often approximated by![]()
where ![]() is frequency,
is frequency, ![]() is series turns per phase, and
is series turns per phase, and ![]() is the fundamental flux per pole (in Webers).
is the fundamental flux per pole (in Webers).
The instantaneous electrical‑to‑mechanical power balance (ignoring losses) is simply![]()
where ![]() is electromagnetic torque and
is electromagnetic torque and ![]() is mechanical angular speed (rad/s).
is mechanical angular speed (rad/s).
3) A clean, practical classification (with examples)
3.1 By energy conversion
- Motors
- AC induction motor (IM) — the workhorse of industry
- AC synchronous motor (SM) — precise speed, high power factor correction capability
- DC motor — easy torque control, used in legacy systems and some special applications
- Brushless DC / Permanent‑magnet synchronous motor (BLDC/PMSM) — high efficiency, high power density
- Generators
- Synchronous generator (a.k.a. alternator) — dominant in large power plants
- Induction generator — used in some wind and small hydro
- Transformers
- Power transformers — transmission/distribution interface
- Instrument transformers — CTs and PTs for measurement & protection
- Special transformers — autotransformers, phase‑shifting, rectifier transformers
3.2 By construction
- Rotating machines — motors/generators (rotor + stator)
- Static machines — transformers
3.3 By excitation / commutation
- DC machines — commutator/brush based
- AC machines
- Synchronous (field winding or permanent magnets)
- Asynchronous (induction)
3.4 By power scale & duty
- Fractional‑horsepower to multi‑hundred‑megawatt turbo‑generators
- Continuous, intermittent, short‑time duty (as per IEC/IEEE duty classes)
4) Where do electrical machines sit inside the power system?
Let’s walk the power system from generation → transmission → distribution → loads and place each machine.
- Generation (plants)
- Synchronous generators (steam, gas, hydro, nuclear): they set system frequency and voltage (via excitation systems and governors).
- Large step‑up transformers immediately raise voltage for transmission.
- Transmission
- Power transformers at substations for voltage transformation (e.g., 345 kV ↔ 154 kV ↔ 22.9 kV, etc.).
- Rotating machines are rare here, but synchronous condensers (a motor running over‑excited) can provide dynamic VAR support.
- Distribution
- Distribution transformers (pole‑mounted, pad‑mounted) feeding medium- to low-voltage networks.
- Voltage regulators, on-load tap changers (OLTC) within transformers keep bus voltages inside limits.
- End‑use / Loads
- Induction motors (fans, pumps, compressors, conveyors) dominate industrial and commercial load.
- Synchronous motors (large compressors, mills) when power factor correction or constant speed is required.
- Adjustable-speed drives (ASDs) + PMSMs/IMs in modern high‑efficiency applications.
- Renewables & Storage
- Doubly-fed induction generators (DFIGs) and full-converter PM machines in wind turbines.
- Synchronous machines still appear in some hydro and pumped storage.
- Transformers everywhere between inverter stages and the grid.
5) Nameplate & performance quantities you must know
- Rated apparent power
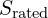 (VA, kVA, MVA)
(VA, kVA, MVA) - Rated voltage/current (line/phase, RMS)
- Frequency
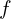 (50/60 Hz typically)
(50/60 Hz typically) - Speed (r/min) or number of poles
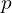
- Efficiency
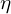
- Power factor
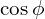 (motors usually lagging, synchronous condenser can lead)
(motors usually lagging, synchronous condenser can lead) - Temperature rise / insulation class
- Short-circuit impedance (transformers), per-unit reactances (machines)
6) Modeling snippets you’ll see everywhere
6.1 Synchronous speed (for AC machines)
![]()
6.2 Induction motor slip
![]()
6.3 Transformer ideal ratio
![]()
6.4 Input, output, losses, efficiency
![]()
7) Three worked example problems
▶ Beginner (apparent power, power factor, efficiency)
Problem
A 3‑phase induction motor delivers ![]() at an efficiency of
at an efficiency of ![]() and power factor
and power factor ![]() (lagging). What is the apparent input power
(lagging). What is the apparent input power ![]() ?
?
Solution
- Input power:
![]()
Apparent input power:
![]()
Answer: ![]() .
.
▶ Intermediate (synchronous speed, slip, rotor speed)
Problem
A 4‑pole, 60 Hz induction motor runs at ![]() under load. Find the synchronous speed, slip, and electrical frequency of the rotor currents.
under load. Find the synchronous speed, slip, and electrical frequency of the rotor currents.
Solution
- Synchronous speed:
![]()
Slip:
![]()
Rotor current frequency:
![]()
Answers: ![]() .
.
▶ Advanced (synchronous generator torque & mechanical power)
Problem
A 3‑phase, 50 Hz synchronous generator delivers ![]() at
at ![]() (lagging). The turbine drives it at
(lagging). The turbine drives it at ![]() . Assume total losses are 2% of output power. Compute the mechanical input power and shaft torque.
. Assume total losses are 2% of output power. Compute the mechanical input power and shaft torque.
Solution
- Real output power:
![]()
Losses:
![]()
Mechanical input power:
![]()
Angular speed:
![]()
Shaft torque:
![]()
Answers:![]() .
.
8) Quick glossary (symbols you just saw)
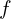 : electrical frequency (Hz)
: electrical frequency (Hz)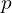 : number of poles
: number of poles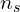 : synchronous speed (r/min)
: synchronous speed (r/min)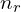 : rotor speed (r/min)
: rotor speed (r/min) : slip
: slip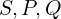 : apparent, real, reactive power
: apparent, real, reactive power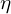 : efficiency
: efficiency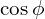 : power factor
: power factor : mechanical angular speed (rad/s)
: mechanical angular speed (rad/s)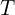 : torque (N·m)
: torque (N·m)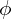 : magnetic flux (Wb)
: magnetic flux (Wb)
9) Common mistakes to avoid
- Calling every motor “induction”: synchronous and PM machines are widely used, especially with drives.
- Ignoring power factor: it matters for sizing feeders, transformers, and converters.
- Forgetting rotor current frequency = s f in induction machines.
- Treating transformers as lossless when calculating voltage regulation and short‑circuit current.
10) TL;DR cheat sheet
- Electrical machine = motor, generator, or transformer.
- Induction motors dominate loads; synchronous generators dominate central generation.
- Transformers glue the voltage levels together at every stage.
- First equations to remember:
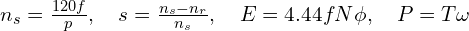 .
.

Leave a Reply