1. 왜 회로 해석을 하는가: 목적의 분해
회로 해석(circuit analysis)은 단순히 ![]() 을 계산하는 행위를 넘어, 설계 의사결정의 근거를 만들고, 제품의 위험을 낮추며, 비용을 줄이는 전 과정을 의미합니다. 대표적인 목적은 다음과 같습니다.
을 계산하는 행위를 넘어, 설계 의사결정의 근거를 만들고, 제품의 위험을 낮추며, 비용을 줄이는 전 과정을 의미합니다. 대표적인 목적은 다음과 같습니다.
- 성능 예측 및 검증
- 목표 대역폭, 이득, 노이즈, 전압 강하, 과도 응답 등을 사전 계산/시뮬레이션으로 확인합니다.
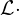 (라플라스 변환),
(라플라스 변환), 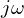 (주파수 해석) 등을 이용해 시간-주파수 영역에서 일관되게 본질을 파악합니다.
(주파수 해석) 등을 이용해 시간-주파수 영역에서 일관되게 본질을 파악합니다.
- 안정성·안전성 평가
- 전력 회로에서 소자 정격(
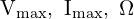 ) 대비 여유가 충분한지, 발진 가능성이 없는지, 보호 소자가 잘 동작하는지 확인합니다.
) 대비 여유가 충분한지, 발진 가능성이 없는지, 보호 소자가 잘 동작하는지 확인합니다.
- 전력 회로에서 소자 정격(
- 최적화(비용/전력/면적/EMI)
- 필요한 사양을 만족하면서 부품 수, 손실, 발열, EMI/EMC를 최소화합니다. 예: 스위칭 주파수
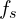 선택, 인덕터 리플 전류
선택, 인덕터 리플 전류 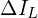 제한,
제한, 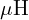 단위의 소자 선택.
단위의 소자 선택.
- 필요한 사양을 만족하면서 부품 수, 손실, 발열, EMI/EMC를 최소화합니다. 예: 스위칭 주파수
- 모델링/추상화
- 실제 복잡한 서브시스템을 테브난/노턴 등가(
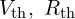 )로 줄여 시스템 레벨 해석 및 제어기 설계에 사용합니다.
)로 줄여 시스템 레벨 해석 및 제어기 설계에 사용합니다.
- 실제 복잡한 서브시스템을 테브난/노턴 등가(
- 디버깅/트러블슈팅 가속화
- 실측 파형이 기대 식(
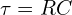 ,
, 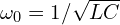 )과 다를 때, 원인(기생
)과 다를 때, 원인(기생 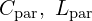 , 접지 임피던스 등)을 구조적으로 좁혀 나갈 수 있습니다.
, 접지 임피던스 등)을 구조적으로 좁혀 나갈 수 있습니다.
- 실측 파형이 기대 식(
2. 무엇을 어떻게 계산하나: 대표 해석 기법
- 기본법칙 기반(키르히호프 법칙, 옴의 법칙)
- KCL/KVL을 이용한 노달 분석(
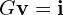 )과 루프(메시) 분석(
)과 루프(메시) 분석(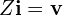 )은 여전히 가장 보편적인 수작업/상징 해석 기법입니다.
)은 여전히 가장 보편적인 수작업/상징 해석 기법입니다.
- KCL/KVL을 이용한 노달 분석(
- 선형화, 등가 변환
- 테브난/노턴 등가회로, 수퍼포지션,
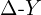 변환 등을 통해 복잡도를 낮춥니다.
변환 등을 통해 복잡도를 낮춥니다.
- 테브난/노턴 등가회로, 수퍼포지션,
- 주파수 영역 해석
- 푸리에/라플라스 변환으로 전달함수
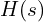 , 보데 플롯, 위상 여유/이득 여유를 구해 안정성과 응답 특성을 평가합니다.
, 보데 플롯, 위상 여유/이득 여유를 구해 안정성과 응답 특성을 평가합니다.
- 푸리에/라플라스 변환으로 전달함수
- 상태공간(state-space) 해석
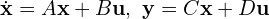
- 제어기 설계, MIMO 전력 변환기, 고차 필터에서 필수적입니다.
- 확률/통계적 해석
- 공정 편차, 온도 변화(
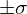 )를 포함한 몬테카를로 분석으로 신뢰도를 평가합니다.
)를 포함한 몬테카를로 분석으로 신뢰도를 평가합니다.
- 공정 편차, 온도 변화(
- 수치 시뮬레이션(SPICE 계열, AMS, EM Co-sim)
- 트랜지언트, AC, 노이즈, S-파라미터(
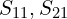 ) 등 실측에 가까운 결과를 신속히 얻습니다.
) 등 실측에 가까운 결과를 신속히 얻습니다.
- 트랜지언트, AC, 노이즈, S-파라미터(
3. 어디에서 쓰이나: 응용 분야 스펙트럼
- 아날로그/혼성 신호
- 증폭기, ADC/DAC 프런트엔드, 필터, PLL.
- 잡음 해석(
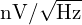 ), 지터, 선형성(THD, SFDR)을 정량화합니다.
), 지터, 선형성(THD, SFDR)을 정량화합니다.
- 디지털/고속 인터페이스
- SI/PI(signal/power integrity). 전송선로의 특성 임피던스
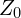 , 반사 계수
, 반사 계수 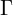 , 아이 다이어그램 분석.
, 아이 다이어그램 분석.
- SI/PI(signal/power integrity). 전송선로의 특성 임피던스
- 전력전자(SMPS, Inverter, DAB 등)
- 듀티비
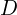 , 효율
, 효율 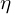 , 스위칭 손실, 인덕터/커패시터 전류 리플, 루프 보상 설계(
, 스위칭 손실, 인덕터/커패시터 전류 리플, 루프 보상 설계(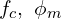 ).
).
- 듀티비
- RF/마이크로파
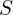 -파라미터, 잡음지수(NF), IP3, Q-인자, 매칭 네트워크 해석.
-파라미터, 잡음지수(NF), IP3, Q-인자, 매칭 네트워크 해석.
- 임베디드/IoT 전원 설계
- 배터리 수명 예측, LDO 안정성(ESR 제약), 부트스트랩/소프트스타트.
- 안전/산업 규격 대응
- 과전압/과전류/서지 해석, 절연 내압,
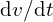 ,
, 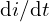 스트레스 평가.
스트레스 평가.
- 과전압/과전류/서지 해석, 절연 내압,
4. 실무 워크플로: “손 계산 → 1차 모델 → 시뮬레이션 → 실측”의 폐루프
- 손 계산으로 질서 정리
- 차수, 지배 극점, 근사식(예:
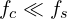 )을 먼저 잡아 직관을 확보합니다.
)을 먼저 잡아 직관을 확보합니다.
- 차수, 지배 극점, 근사식(예:
- 1차 모델로 리스크 컷오프
- 테브난 등가, 소자 이상적 가정으로 구현 용량/전력/발열을 가늠합니다.
- 세부 SPICE/EM 시뮬레이션
- 기생 RLC, 패드/패키지 모델, 컴팩트 모델 반영.
- 프로토타이핑 & 실측 비교
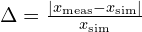 으로 오차를 추적하고, 모델을 갱신합니다.
으로 오차를 추적하고, 모델을 갱신합니다.
5. 예제 문제 6선 (초급 2, 중급 2, 고급 2) — 모두 해설 포함
■ 초급 1: 단일 저항 회로 전류 계산
문제
전압원 ![]() 와 저항
와 저항 ![]() 가 직렬로 연결되었다. 전류
가 직렬로 연결되었다. 전류 ![]() 를 구하라.
를 구하라.
해설
![]()
■ 초급 2: 전압 분배기
문제![]() ,
, ![]() ,
, ![]() 인 분압기에서
인 분압기에서 ![]() 을 구하라.
을 구하라.
해설
![]()
■ 중급 1: RLC 직렬 공진 주파수
문제
직렬 RLC 회로에서 ![]() ,
, ![]() 일 때, 공진 각주파수
일 때, 공진 각주파수 ![]() 와 공진 주파수
와 공진 주파수 ![]() 를 구하라.
를 구하라.
해설![]()
![]()
■ 중급 2: 테브난 등가 회로
문제
독립 전압원 ![]() 가
가 ![]() 에 직렬로 연결되어 있고, 그 출력 노드에서
에 직렬로 연결되어 있고, 그 출력 노드에서 ![]() 이 접지로 연결되어 있다. 출력 노드에서 본 테브난 등가
이 접지로 연결되어 있다. 출력 노드에서 본 테브난 등가 ![]() 를 구하라.
를 구하라.
해설
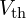 은
은 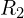 가 로드일 때의 출력 전압:
가 로드일 때의 출력 전압:
![]()
![]() 는 소스를 0(이상적 전압원 → 단락)으로 만들고 본 등가 저항:
는 소스를 0(이상적 전압원 → 단락)으로 만들고 본 등가 저항:
![]()
■ 고급 1: 상태공간으로 본 RLC 2차 회로
문제
직렬 RLC 회로(입력 전압 ![]() , 출력은 커패시터 전압
, 출력은 커패시터 전압 ![]() )에 대해 상태 변수를
)에 대해 상태 변수를 ![]() 로 정의하라. 상태방정식
로 정의하라. 상태방정식 ![]() ,
, ![]() 를 유도하라.
를 유도하라.
해설(개략)
직렬 RLC에서
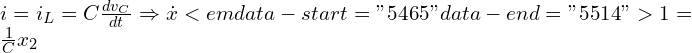
KVL로
![]()
따라서
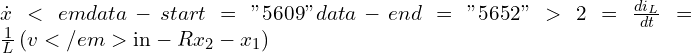
행렬 형태:![]()
![]()
■ 고급 2: 벅 컨버터(Buck Converter) 리플 전류와 듀티비
문제
이상적 벅 컨버터에서 입력 전압 ![]() , 출력 전압
, 출력 전압 ![]() , 스위칭 주파수
, 스위칭 주파수 ![]() , 인덕턴스
, 인덕턴스 ![]() 일 때,
일 때,
- 듀티비
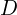 ,
, - 인덕터 리플 전류
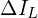 (CCM 가정)을 구하라.
(CCM 가정)을 구하라.
해설
- 듀티비 (이상적, 손실 무시):
![]()
리플 전류:
![]()
6. 마무리: “계산-모델-시뮬-실측”의 반복이 품질을 만든다
회로 해석의 가치는, 한 번의 “정답”을 구하는 데 있지 않습니다. 설계 초기의 근사식, 중간 단계의 상징해석/주파수 해석, 최종 단계의 숫자 시뮬레이션과 실측 간 편차를 체계적으로 줄여가는 일련의 폐루프 과정이 곧 해석의 본질입니다.
실무자는 이 루프를 빠르게 돌릴 수 있는 **도구(수학, 모델, 시뮬레이터, 측정 장비)와 판단 기준(여유도, 민감도, worst-case)**을 갖추어야 하며, 그것이 제품의 신뢰성과 비용 경쟁력을 결정합니다.

Leave a Reply