1. 트랜스포머란 무엇인가?
트랜스포머(Transformer)는 전기 에너지를 한 회로에서 다른 회로로 변환할 때 전압과 전류를 바꾸는 전기기기입니다. 주로 교류 전원에 사용하며, 전압의 크기를 높이거나 낮출 때 쓰입니다.
트랜스포머는 기본적으로 두 개 이상의 권선으로 구성되어 있고, 자기장을 통해 전기적 에너지를 전달합니다. 자기장의 변화가 다른 권선에 유도 기전력을 발생시켜 전력을 전송합니다.
2. 트랜스포머의 기본 원리와 작동 방식
트랜스포머의 동작은 
에 의거합니다. 1차 권선에 교류 전압이 인가되면, 그 전류가 변화하는 자기장을 생성하고, 이 자기장이 2차 권선에 유도기전력을 발생시킵니다.
여기서,
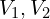는 각각 1차, 2차 전압
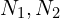는 각각 1차, 2차 권선 수
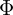는 자기 플럭스(자기 선속)입니다.
즉, 권선 수 비에 따라 전압이 변하는 원리입니다.
3. 이상적인 트랜스포머 모델
이상적인 트랜스포머는 손실이 없고, 자기 누설이나 저항 등이 없다고 가정합니다. 이에 따라 다음과 같은 관계가 성립합니다.
여기서 
는 변압비(turns ratio)입니다.
또한, 전력 보존법칙에 따라,
전류는 변압비의 역수로 바뀝니다.
4. 실제 트랜스포머의 등가회로
실제 트랜스포머는 권선 저항, 누설 리액턴스, 자기 손실, 철손 등 다양한 손실 요소가 존재합니다. 이를 반영해 등가회로를 구성합니다.
4.1 권선 저항 (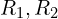
)
1차, 2차 권선의 저항이며, 전력 손실과 열 발생을 일으킵니다.
4.2 누설 리액턴스 (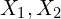
)
권선 주변의 누설 자기장에 의해 발생하는 임피던스입니다.
4.3 철손 (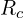
)
트랜스포머 철심에서 발생하는 손실을 저항으로 모델링합니다.
4.4 자기 리액턴스 (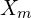
)
철심의 자화에 의한 리액턴스로, 이상적인 자기 유도와 달리 자기 포화 효과 등을 포함합니다.
5. 등가회로 표현과 2차측 임피던스 반사
트랜스포머 회로 해석을 편리하게 하기 위해 2차 권선의 임피던스를 1차측으로 반사시키는 작업을 합니다. 이는 다음과 같이 표현합니다.
여기서,
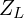는 2차측 부하 임피던스
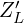는 1차측에 반사된 임피던스입니다.
이를 통해 모든 임피던스를 1차측 등가회로에 모아 해석이 가능합니다.
6. 트랜스포머 회로 해석 절차
- 2차측 부하 임피던스 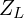를 변압비 제곱
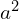로 곱해 1차측 등가 임피던스 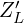로 변환합니다. - 1차측 권선 저항, 누설 리액턴스와 부하 임피던스 반사값을 직렬 연결하여 전체 임피던스 계산.
- 1차측 전압과 전체 임피던스를 이용해 1차 전류를 계산.
- 2차 전류는 1차 전류와 변압비 관계로 계산.
- 각 전압, 전류, 전력 등을 산출하여 회로 상태를 분석.
7. 대표 수식 정리
- 변압비:
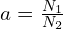
- 임피던스 반사:
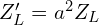
- 1차 등가 임피던스:
1차 전류:
2차 전류:
8. 회로도 예제
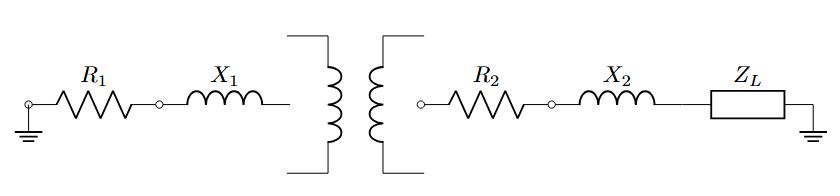
9. 트랜스포머 회로 해석 실전 예시
문제:
1차 전압 
, 변압비 
인 트랜스포머가 있습니다. 2차측 부하 임피던스는 
입니다. 1차측 권선 저항과 누설 리액턴스는 각각 
일 때, 1차 전류를 구하시오.
풀이:
- 2차 임피던스를 1차측으로 반사:
- 전체 임피던스:
- 1차 전류:
복소수 분모 유리화 등으로 계산 가능합니다.
10. 마무리 정리
트랜스포머 회로 해석은 변압비에 따른 임피던스 반사와 권선 특성을 반영한 등가회로를 이해하는 것이 핵심입니다. 이를 통해 복잡한 회로도 쉽게 해석할 수 있고, 전력 시스템에서 중요한 역할을 수행합니다. 초보자도 기본 원리와 수식을 숙지하면 충분히 실무 적용이 가능합니다.
Leave a Reply