1. 개요

회로 해석에서 복잡한 회로망을 간단한 등가 회로로 대체할 수 있다는 것은 매우 강력한 수단입니다. 그중에서도 **테브난 정리(Thevenin’s Theorem)**와 **노튼 정리(Norton’s Theorem)**는 다양한 전기전자 회로 해석에서 핵심적인 역할을 합니다.

2. 테브난 정리 (Thevenin’s Theorem)

테브난 정리에 따르면, 임의의 선형 2단자 회로는 하나의 **전압원(V_th)**과 하나의 **직렬 저항(R_th)**으로 대체할 수 있습니다.

📌 적용 절차

1. 출력 단자를 개방(open circuit)하고 개방전압 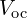계산 → 테브난 전압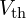
2. 독립전원을 제거하고 저항만 남긴 회로에서 단자 간 저항 계산 → 테브난 저항
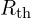
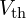3. 와 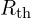를 직렬로 연결 → 등가 회로 완성

📌 수식 요약

---

3. 노튼 정리 (Norton’s Theorem)

노튼 정리는 테브난 정리와 쌍둥이 개념으로, 선형 2단자 회로를 **전류원(I_N)**과 **병렬 저항(R_N)**으로 대체합니다.

📌 적용 절차

1. 단자 간 단락(short circuit) 전류 측정 → 노튼 전류
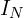
2. 저항 계산은 테브난과 동일 →
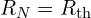
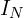3. 과 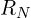을 병렬로 연결 → 노튼 등가 회로 완성

📌 수식 요약

---

4. 테브난과 노튼의 관계

   

즉, 두 회로는 동일한 외부 부하에 대해 동일한 전압과 전류를 제공합니다.

---

5. 실제 예시

예제 회로 설명

• 전원:
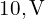
• 직렬 저항:
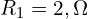
• 분기 저항:
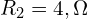
• 부하 저항:

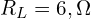
이 회로에서 테브난 등가 회로를 구하면:

• 
• 

---

6. 활용 분야

• 복잡한 회로에서 부하 변화에 따른 영향 분석
• 전력 전달 효율 계산
• 시스템 최적화 및 검증

중첩의 원리(Superposition)의 이해와 회로 해석 완전 정복

메시 전류법 완벽 정리: 회로 해석의 기초부터 고급 예제까지

노드 전압법 완벽 정리: 초보자도 이해하는 회로 해석 기본