임피던스와 어드미턴스 완전 정복
1. 서론: 교류 회로에서의 저항 그 이상
직류 회로에서는 저항(Resistance)이 전류의 흐름을 방해하는 유일한 요소입니다. 하지만 교류 회로에서는 전류의 크기뿐 아니라 위상까지 영향을 주는 여러 요소가 작용하게 됩니다. 이때 등장하는 개념이 바로 ‘임피던스(Impedance)’와 ‘어드미턴스(Admittance)’입니다. 이 두 가지는 교류 회로 해석의 핵심이며, 복소수 표현을 통해 전압과 전류의 위상 관계를 정확하게 설명할 수 있습니다.
2. 임피던스란 무엇인가?
임피던스는 교류 회로에서 전류의 흐름을 방해하는 정도를 나타냅니다. 직관적으로는 교류 회로에서의 저항이라고 생각할 수 있지만, 더 나아가 위상차까지 고려해야 하므로 복소수로 표현됩니다.
▷ 임피던스의 정의
![]()
여기서
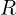 : 저항(실수 성분)
: 저항(실수 성분)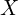 : 리액턴스(허수 성분)
: 리액턴스(허수 성분)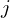 : 허수 단위로,
: 허수 단위로, 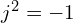
3. 리액턴스와 그 유형
리액턴스는 전압과 전류 사이에 위상차를 발생시키는 성분입니다. 이는 커패시터나 인덕터에 의해 발생하며, 다음과 같이 정의됩니다:
- 인덕터의 리액턴스
![]()
커패시터의 리액턴스
![]()
여기서 ![]() 는 각주파수입니다.
는 각주파수입니다.
4. 임피던스의 종류별 표현
- 저항
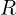 :
: 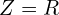
- 인덕터
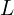 :
: 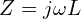
- 커패시터
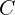 :
: 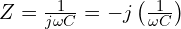
5. 어드미턴스란?
어드미턴스는 임피던스의 역수이며, 전류가 얼마나 잘 흐를 수 있는지를 나타냅니다. 단위는 지멘스(Siemens, ![]() )입니다.
)입니다.
![]()
여기서
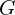 : 컨덕턴스(저항의 역수)
: 컨덕턴스(저항의 역수)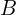 : 서셉턴스(리액턴스의 역수 성분)
: 서셉턴스(리액턴스의 역수 성분)
6. 임피던스와 어드미턴스 관계 예제
![]()
분모 유리화:
![]()
즉,
![]()
7. 교류 회로에서의 활용
직렬 회로의 임피던스 합
![]()
병렬 회로의 어드미턴스 합
![]()
8. 임피던스 벡터와 페이저 표현
교류 회로에서 전압과 전류는 사인파 또는 코사인파로 표현되며, 이들은 페이저로 변환되어 분석됩니다.
예:
![]()
이때 임피던스는 페이저 전압과 전류의 비로 정의됩니다.
![]()

Leave a Reply