1. 노드 전압법(Node Voltage Method)이란?
노드 전압법은 전기회로 해석에서 가장 널리 쓰이는 방법 중 하나로, 회로 내 노드(접점)들의 전압을 미지수로 설정해 방정식을 세우고 해를 구하는 방법입니다.
기본 아이디어는 다음과 같습니다.
- 회로 내 모든 전압원의 한쪽 기준점(보통 접지, 그라운드)을 정합니다.
- 나머지 노드들의 전압을 미지수로 둡니다.
- 키르히호프 전류법칙(KCL)에 따라 각 노드에서 유입 전류와 유출 전류의 합이 0이 되는 방정식을 세웁니다.
- 이 연립방정식을 풀어 노드 전압을 구합니다.
2. 노드 전압법의 장점
- 회로 내 전류 변수를 일일이 계산할 필요 없이 노드 전압 변수만 다루어 계산량이 줄어듭니다.
- 여러 개의 전압원이 있어도 체계적으로 방정식을 세울 수 있습니다.
- 복잡한 회로 해석에 효과적이며 컴퓨터 프로그램 구현에 적합합니다.
3. 노드 전압법 기본 절차
- 접지 노드 설정
- 회로에서 기준 전압(0V)을 정하는 노드를 하나 선택합니다. 보통 가장 많은 연결선이 있는 노드를 접지로 선택합니다.
- 노드 전압 변수 설정
- 접지 노드를 제외한 모든 노드 전압을 변수로 설정합니다.
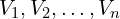 형태로 표기합니다.
형태로 표기합니다.
- 접지 노드를 제외한 모든 노드 전압을 변수로 설정합니다.
- 키르히호프 전류법칙(KCL) 적용
- 각 노드에서 유입 전류와 유출 전류 합이 0이 되도록 전류 식을 세웁니다.
- 저항은 옴의 법칙에 의해 전류 = 전압차 / 저항으로 표현합니다. 예를 들어, 노드 1과 접지 사이에 저항
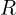 가 있으면 전류는
가 있으면 전류는 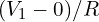 입니다.
입니다.
- 연립방정식 작성 및 풀이
- 노드별 KCL식을 모아 연립방정식을 만듭니다.
- 행렬식이나 가우스 소거법, 계산기 등을 활용해 풀어 노드 전압을 구합니다.
- 전류 및 다른 변수 계산
- 구한 노드 전압을 활용해 회로 내 전류 및 기타 변수들을 계산할 수 있습니다.
4. 노드 전압법 적용 시 주의사항
- 전압원이 두 노드를 직접 연결하는 경우 슈퍼노드(supernode)를 만들어야 합니다.
- 전류원이 있는 경우에는 해당 노드에 전류원 조건을 추가해야 합니다.
- 노드 수가
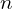 개면, 접지 노드를 제외한
개면, 접지 노드를 제외한  개의 노드전압 변수를 구해야 합니다.
개의 노드전압 변수를 구해야 합니다.
5. 노드 전압법 예제 문제
초급 문제 1
회로에 접지 노드와 노드 1이 있습니다. 노드 1과 접지 사이에 저항 ![]() , 노드 1과 접지 사이에 전압원
, 노드 1과 접지 사이에 전압원 ![]() 가 있습니다. 노드 1의 전압을 구하세요.
가 있습니다. 노드 1의 전압을 구하세요.
풀이
전압원이 노드 1과 접지를 직접 연결하므로 노드 1 전압은 바로 ![]() 와 같습니다.
와 같습니다.
답: ![]()
초급 문제 2
저항 ![]() ,
, ![]() 가 접지 노드와 노드 1, 노드 2 사이에 각각 연결되어 있습니다. 노드 1과 노드 2 사이에는 저항
가 접지 노드와 노드 1, 노드 2 사이에 각각 연결되어 있습니다. 노드 1과 노드 2 사이에는 저항 ![]() 이 있습니다. 노드 1에 전류원
이 있습니다. 노드 1에 전류원 ![]() 가 연결되어 있고, 접지는 0V로 설정되어 있습니다. 노드 1과 노드 2 전압을 구하세요.
가 연결되어 있고, 접지는 0V로 설정되어 있습니다. 노드 1과 노드 2 전압을 구하세요.
풀이
접지를 기준으로 노드 전압 ![]() 를 미지수로 설정.
를 미지수로 설정.
KCL식 (노드 1):
![]()
KCL식 (노드 2):
![]()
값 대입 후 연립방정식 풀기.
(1) ![]()
(2) ![]()
식 (2) 정리:![]()
![]()
식 (1) 대입:
![]()
따라서,
![]()
![]()
답:
![]()
중급 문제 1
다음 회로에서, 접지를 기준으로 노드 1과 노드 2 전압을 구하시오.
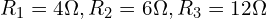
- 노드 1과 접지 사이에 전압원
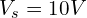
- 노드 2와 접지 사이에 전류원
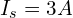
- 노드 1과 노드 2 사이에 저항
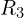
풀이
- 노드 1 전압은
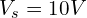 (전압원 직접 연결).
(전압원 직접 연결). - 노드 2 전압
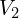 미지수로 두고, 노드 2에 KCL 적용:
미지수로 두고, 노드 2에 KCL 적용:
![]()
값 대입:![]()
![]()
![]()
답:
![]()
중급 문제 2
3노드 회로에서 접지를 기준으로 다음을 구하시오.
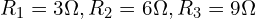
- 노드 1과 접지 사이에 전류원
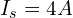
- 노드 2와 접지 사이에 전압원
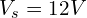
- 노드 1과 노드 2 사이 저항
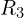
풀이
- 노드 2 전압:
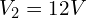 (전압원 직접 연결).
(전압원 직접 연결). - 노드 1 전압
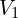 미지수로 두고 KCL:
미지수로 두고 KCL:
![]()
![]()
![]()
답:
![]()
고급 문제 1
아래 회로에서 접지를 기준으로 노드 1, 노드 2, 노드 3 전압을 구하시오.
- 저항:
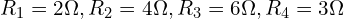
- 노드 1과 접지 사이 전압원:
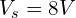
- 노드 2에 전류원:
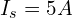
- 연결: 노드 1–노드 2:
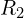 , 노드 2–노드 3:
, 노드 2–노드 3: 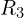 , 노드 3–접지:
, 노드 3–접지: 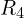 , 노드 1–접지:
, 노드 1–접지: 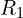
풀이
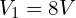 (전압원).
(전압원).- 미지수:
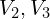
- KCL 노드 2:
![]()
KCL 노드 3:
![]()
식 1:![]()
식 2:
![]()
식 2 정리:
![]()
식 1에 대입:![]()
![]()
따라서,
![]()
![]()
답:
![]()
고급 문제 2
다음 회로에서, 노드 1, 노드 2, 노드 3 전압을 구하시오.
- 저항:
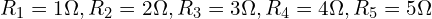
- 전압원: 노드 1과 접지 사이
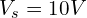
- 전류원: 노드 3에
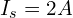
- 연결:
- 노드 1–노드 2:
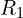
- 노드 2–접지:
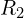
- 노드 2–노드 3:
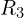
- 노드 3–접지:
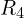
- 노드 1–접지:
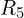
- 노드 1–노드 2:
풀이
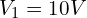 (전압원).
(전압원).- 미지수:
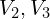
노드 2 KCL:
![]()
노드 3 KCL:
![]()
식 1:![]()
통분 후:![]()
![]()
식 2:![]()
![]()
연립방정식:
![]()
가우스 소거법 또는 행렬법으로 풀면,
- 식1 *7:
![]()
식2 * 2:
![]()
두 식 합:
![]()
식1에 대입:
![]()
답:
![]()
6. 요약 및 활용
노드 전압법은 복잡한 회로 해석을 체계적이고 효율적으로 할 수 있게 하는 방법입니다.
실제 설계나 분석 시 기본으로 숙지하면 회로의 동작을 정량적으로 이해하고 문제를 빠르게 해결하는 데 큰 도움이 됩니다.

Leave a Reply