교류(AC) 회로에서는 전압과 전류가 시간에 따라 계속 변화합니다. 특히 이들이 위상 차이를 가지는 경우, 단순히 
공식을 사용하는 것만으로는 실제 에너지가 얼마만큼 전달되고 소비되는지를 파악할 수 없습니다. 이러한 이유로 전력은 교류 회로에서 더 정교하게 분류되며, 대표적으로 유효전력(Active Power), 무효전력(Reactive Power), 피상전력(Apparent Power) 이라는 개념이 사용됩니다.
이 글에서는 위 세 가지 전력 개념을 기초부터 고급까지 단계적으로 설명하고, 수식과 회로, 그리고 실제 예제를 통해 이해를 도울 것입니다.
1. 교류 회로에서의 전압과 전류
먼저 교류 전압과 전류의 일반적인 표현식을 확인해보겠습니다.
- 전압:
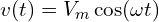
- 전류:
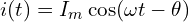
여기서,
, 
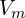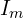은 전압과 전류의 최대값(peak),
는 각주파수(단위: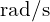 
),
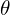는 전압에 대한 전류의 위상차입니다.
전압과 전류의 위상차 가 존재한다면, 두 파형은 동시에 최대값에 도달하지 않으며, 에너지 전달에 비효율이 발생합니다.
2. 유효전력 (Active Power,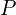 
)
유효전력은 실제로 전기 에너지가 소비되는 전력을 의미합니다. 저항 성분에 의해 소모되며, 열로 전환되거나 기계적 에너지로 전환되는 에너지입니다.
공식:
여기서 
, 
는 전압과 전류의 실효값입니다. 
는 전력 계수(power factor)라고 불리며, 에너지가 얼마나 효과적으로 소비되는지를 나타냅니다.
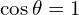: 모든 전력이 소비됨 (순수 저항)
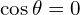: 실제 소비 전력 없음 (순수 유도/용량)
3. 무효전력 (Reactive Power,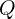 
)
무효전력은 실제 에너지가 전달되지 않지만, 교류 특성상 회로에서 교환되며 존재하는 전력입니다. 주로 인덕터나 커패시터에 의해 발생하며, 전력 계통의 부하 특성을 결정합니다.
공식:
단위는 
이며, 실질적인 전력 소비는 하지 않지만 전류를 흐르게 하며 전력 계통의 부하율을 높이는 원인이 됩니다.
4. 피상전력 (Apparent Power,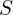 
)
피상전력은 유효전력과 무효전력을 합친 개념이며, 단순히 전압과 전류의 실효값을 곱하여 계산합니다.
공식:
단위는 
이며, 교류 회로의 전체 전력 흐름의 크기를 의미합니다.
5. 전력 삼각형
세 가지 전력의 관계는 다음과 같은 직각 삼각형으로 표현할 수 있습니다.
여기서,
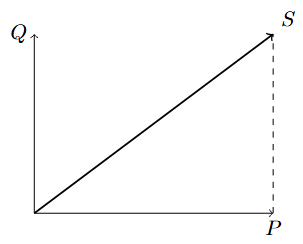
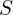- : 피상전력 (빗변)
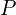- : 유효전력 (밑변)
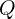- : 무효전력 (높이)
6. 전력 계수 (Power Factor)
전력 계수가 1에 가까울수록 전력이 효율적으로 소비되고 있다는 의미입니다. 산업 현장이나 전력 계통에서는 이 계수를 높이는 것이 매우 중요합니다.
7. 예제 계산
예제 회로:
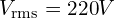
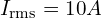
- 위상차
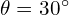
유효전력:
무효전력:
피상전력:
임피던스와 어드미턴스 완전 정복: 복소수 교류 회로 해설
Leave a Reply